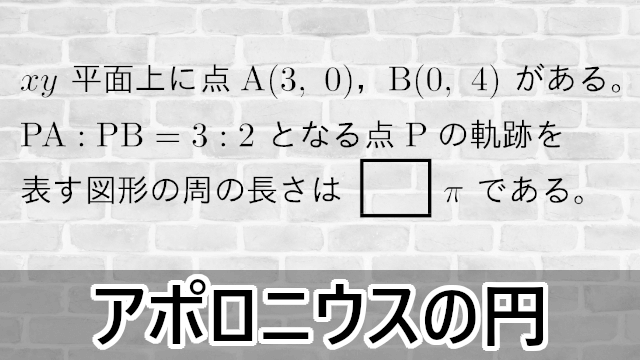
ここでは2定点からの距離の比が一定である点の軌跡(アポロニウスの円)について説明します。
大学入試では「アポロニウスの円」という名前が出てくることはほとんどなく,単なる軌跡の問題として出題されます。
アポロニウスの円についての知識を得ることで,空欄を埋める形式の試験では短時間で解くことができるため有利になるでしょう。
Contents
アポロニウスの円

ヒロ
「アポロニウスの円」についてはチャート式にも書かれているので,知っている人も多いだろう。
アポロニウスの円2つの定点A,Bに対して,$\text{AP}:\text{BP}=m:n$ となるような点Pの軌跡は円となり,この円をアポロニウスの円という。ただし,$m>0$,$n>0$,$m\neq n$ とする。また,アポロニウスの円は,線分ABを $m:n$ に内分する点と外分する点を直径の両端とする円となる。

ヒロ
このことを知っている人にとっては,答えだけを書けば良い試験であれば,すぐに軌跡を求めることができるため,時間的に有利になるだろう。