ここでは正弦定理と余弦定理を利用して様々な問題を解く方法について説明します。
三角形の辺の長さや角の大きさを求めるためには,正弦定理や余弦定理をうまく使えるようになる必要があります。
問題によっては片方だけでは解けない問題もあります。
状況に応じて対応できる力を身に付けましょう。
三角形の辺と角の決定
問題次の各場合について $\sankaku{ABC}$ の残りの辺の長さと角の大きさを求めよ。
(1) $a=\sqrt{3},~B=45\Deg,~C=15\Deg$
(2) $b=2,~c=\sqrt{3}+1,~A=30\Deg$
(1) $a=\sqrt{3},~B=45\Deg,~C=15\Deg$
(2) $b=2,~c=\sqrt{3}+1,~A=30\Deg$
【(1)の考え方と解答】
(1)では1辺とその両端の角が与えられているから,$\sankaku{ABC}$ は1つに決まる。
三角形の3つの内角のうち,2つが分かっているから残りの角の大きさはすぐに分かる。
(1)では1辺とその両端の角が与えられているから,$\sankaku{ABC}$ は1つに決まる。
三角形の3つの内角のうち,2つが分かっているから残りの角の大きさはすぐに分かる。
\begin{align*}
A&=180\Deg-(B+C) \\[4pt]
&=180\Deg-(45\Deg+15\Deg) \\[4pt]
&=180\Deg-60\Deg=120\Deg
\end{align*}
あとは残りの2辺の長さを求めよう。$A$ と $B$ の三角比の値を簡単に求めることができるから,正弦定理を使えば $b$ を求めることができるね。A&=180\Deg-(B+C) \\[4pt]
&=180\Deg-(45\Deg+15\Deg) \\[4pt]
&=180\Deg-60\Deg=120\Deg
\end{align*}
\begin{align*}
&\dfrac{a}{\sin A}=\dfrac{b}{\sin B} \\[4pt]
&b=\dfrac{\sin B}{\sin A}a
\end{align*}
この式に $A=120\Deg,~B=45\Deg,~a=\sqrt{3}$ を代入すると&\dfrac{a}{\sin A}=\dfrac{b}{\sin B} \\[4pt]
&b=\dfrac{\sin B}{\sin A}a
\end{align*}
\begin{align*}
b&=\dfrac{\sin45\Deg}{\sin120\Deg}\Cdota\sqrt{3} \\[4pt]
&=\dfrac{\sqrt{2}}{2}\Cdota\dfrac{2}{\sqrt{3}}\Cdota\sqrt{3}=\sqrt{2}
\end{align*}
$c$ については,その対角が $C=15\Deg$ のため,$\sin15\Deg$ を求めるのが面倒な場合は,正弦定理を使うのを避けて余弦定理を利用しよう。b&=\dfrac{\sin45\Deg}{\sin120\Deg}\Cdota\sqrt{3} \\[4pt]
&=\dfrac{\sqrt{2}}{2}\Cdota\dfrac{2}{\sqrt{3}}\Cdota\sqrt{3}=\sqrt{2}
\end{align*}
\begin{align*}
&a^2=b^2+c^2-2bc\cos A \\[4pt]
&(\sqrt{3})^2=(\sqrt{2})^2+c^2-2\sqrt{2}c\Cdota\cos120\Deg \\[4pt]
&c^2+\sqrt{2}c-1=0 \\[4pt]
&c=\dfrac{-\sqrt{2}\pm\sqrt{6}}{2}
\end{align*}
$c>0$ より,$c=\dfrac{\sqrt{6}-\sqrt{2}}{2}$&a^2=b^2+c^2-2bc\cos A \\[4pt]
&(\sqrt{3})^2=(\sqrt{2})^2+c^2-2\sqrt{2}c\Cdota\cos120\Deg \\[4pt]
&c^2+\sqrt{2}c-1=0 \\[4pt]
&c=\dfrac{-\sqrt{2}\pm\sqrt{6}}{2}
\end{align*}
(2) $b=2,~c=\sqrt{3}+1,~A=30\Deg$
【(2)の考え方と解答】
2辺とその間の角が与えられているから,三角形が1つに決まる。まずは余弦定理を用いて $a$ を求めよう。
これで3辺の長さが分かったから余弦定理を利用して $B,~C$ を求めよう。
$\cos B$ と $\cos C$ のどちらを求めるかで悩むが,対辺の長さが「複雑でない方」を考えるようにしよう。今回の場合は $b$ と $c$ を比べると $b$ の方が「複雑でない」から $\cos B$ を考える。
三角形の内角の和は180°であるから
2辺とその間の角が与えられているから,三角形が1つに決まる。まずは余弦定理を用いて $a$ を求めよう。
\begin{align*}
a^2&=b^2+c^2-2bc\cos A \\[4pt]
&=2^2+(\sqrt{3}+1)^2-2\Cdota2(\sqrt{3}+1)\cos30\Deg \\[4pt]
&=4+(4+2\sqrt{3})-2\sqrt{3}(\sqrt{3}+1) \\[4pt]
&=2
\end{align*}
$a>0$ より,$a=\sqrt{2}$a^2&=b^2+c^2-2bc\cos A \\[4pt]
&=2^2+(\sqrt{3}+1)^2-2\Cdota2(\sqrt{3}+1)\cos30\Deg \\[4pt]
&=4+(4+2\sqrt{3})-2\sqrt{3}(\sqrt{3}+1) \\[4pt]
&=2
\end{align*}
これで3辺の長さが分かったから余弦定理を利用して $B,~C$ を求めよう。
$\cos B$ と $\cos C$ のどちらを求めるかで悩むが,対辺の長さが「複雑でない方」を考えるようにしよう。今回の場合は $b$ と $c$ を比べると $b$ の方が「複雑でない」から $\cos B$ を考える。
\begin{align*}
\cos B&=\dfrac{c^2+a^2-b^2}{2ca} \\[4pt]
&=\dfrac{(\sqrt{3}+1)^2+(\sqrt{2})^2-2^2}{2\sqrt{2}(\sqrt{3}+1)} \\[4pt]
&=\dfrac{(4+2\sqrt{3})-2}{2\sqrt{2}(\sqrt{3}+1)} \\[4pt]
&=\dfrac{2(1+\sqrt{3})}{2\sqrt{2}(\sqrt{3}+1)}=\dfrac{1}{\sqrt{2}}
\end{align*}
よって,$B=45\Deg$\cos B&=\dfrac{c^2+a^2-b^2}{2ca} \\[4pt]
&=\dfrac{(\sqrt{3}+1)^2+(\sqrt{2})^2-2^2}{2\sqrt{2}(\sqrt{3}+1)} \\[4pt]
&=\dfrac{(4+2\sqrt{3})-2}{2\sqrt{2}(\sqrt{3}+1)} \\[4pt]
&=\dfrac{2(1+\sqrt{3})}{2\sqrt{2}(\sqrt{3}+1)}=\dfrac{1}{\sqrt{2}}
\end{align*}
三角形の内角の和は180°であるから
\begin{align*}
C&=180\Deg-(A+B) \\[4pt]
&=180\Deg-(30\Deg+45\Deg)=105\Deg
\end{align*}
C&=180\Deg-(A+B) \\[4pt]
&=180\Deg-(30\Deg+45\Deg)=105\Deg
\end{align*}

ヒロ
$\cos B$ を計算するときに「分母を有理化せねば!」と思ってはいけない。

そうなんですか?

ヒロ
分母の $\sqrt{3}+1$ が丸ごと約分できることは確定しているからね。

どういうことですか?

ヒロ
これは別の記事でも書いたように,$B$ を求めるために $\cos B$ を求めているのだから,分母に $\sqrt{3}+1$ が丸ごと残ると $B$ を求めることができなくなってしまう。

なるほど・・・

ヒロ
有理化したところで,分子に $\sqrt{3}-1$ が残るから,有理化することに何の意味もないことに気付けるようになろう。

$\cos C$ を求めずに $\cos B$ を計算したのは何故ですか?

ヒロ
辺の長さが「より簡単に感じる方」の対角を調べるとうまくいくからだよ。

ヒロ
大抵の場合は,三角定規の三角形の組合せによって問題が作られているため,辺の長さが複雑な方は,2つの三角形の辺がつながって1つの辺になっている可能性が高いんだ。

ヒロ
説明しておこうか。

お願いします!
【2つの三角形の組み合わせを見つける】
$c=\sqrt{3}+1$ から長さが $\sqrt{3}$ と1の2つの辺がつながっていると考える。まずは $c$ が底辺の長さだと見て,次のように図を描く。

図の黒丸を通り,底辺に垂直な直線(図の破線)上に点Cがあると考える。
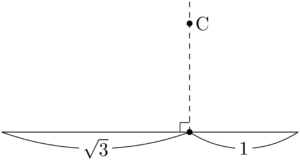
ABを底辺としているため,左右のどちらかがAになり,$A=30\Deg$ であることを考えると,2つの三角形のうち1つは $1:2:\sqrt{3}$ の三角形だと予測できる。$b=2$ だから左側をAにすると,長さをそのままにして $1:2:\sqrt{3}$ の三角形を描くことができる。つまり,次のような図を考えることになる。
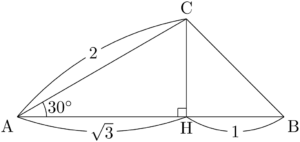
この時点で与えられた条件「$b=2$, $c=\sqrt{3}+1$, $A=30\Deg$」をみたす三角形を描くことができた。
ここで,$\sankaku{ACH}$ に着目すると,$\text{CH}=1$ となるから,$\text{BC}=\sqrt{2}$ となる。
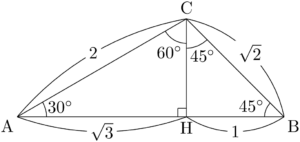
図を描くだけで,大した計算をすることもなく
$c=\sqrt{3}+1$ から長さが $\sqrt{3}$ と1の2つの辺がつながっていると考える。まずは $c$ が底辺の長さだと見て,次のように図を描く。
図の黒丸を通り,底辺に垂直な直線(図の破線)上に点Cがあると考える。

ABを底辺としているため,左右のどちらかがAになり,$A=30\Deg$ であることを考えると,2つの三角形のうち1つは $1:2:\sqrt{3}$ の三角形だと予測できる。$b=2$ だから左側をAにすると,長さをそのままにして $1:2:\sqrt{3}$ の三角形を描くことができる。つまり,次のような図を考えることになる。

この時点で与えられた条件「$b=2$, $c=\sqrt{3}+1$, $A=30\Deg$」をみたす三角形を描くことができた。
ここで,$\sankaku{ACH}$ に着目すると,$\text{CH}=1$ となるから,$\text{BC}=\sqrt{2}$ となる。

図を描くだけで,大した計算をすることもなく
\begin{align*}
a=\sqrt{2},~B=45\Deg,~C=105\Deg
\end{align*}
であることが分かる。a=\sqrt{2},~B=45\Deg,~C=105\Deg
\end{align*}

この考え方を身に付けるには,ある程度の経験が必要かもしれないですね・・・

ヒロ
頑張ろう!

ヒロ
このような考え方を利用した図の描き方をもっと経験したい場合は,次の記事が参考になるだろう。

2003年 センター試験 数学IA 図形【三角比の値を利用した描画】
三角比の値を与えられたときの図の描き方を説明します。この図の描き方をマスターすることで,問題を見る前に,答えを求めることが出来る問題もあります。しっかり記事を読んで考え方を身に付けましょう。

マーク模試過去問 数学IA 図形【正弦の値を利用した描画】
正弦の値を利用した描画方法について説明します。余弦の値が与えられたときより,少しだけ難しくなります。ただ,出題者が最初に描いたであろう図を最初に描くことができるため,その後の問題にスムーズに答えられるようになります。

ヒロ
ちなみに余弦定理ではなく,正弦定理を利用することもできる。
【(2)の別の考え方と解答】
1組の向かい合う角の大きさと辺の長さが分かったから,正弦定理を利用して残りの角の大きさを求めよう。
ABの長さは $c=\sqrt{3}+1$ で少し複雑なので,より簡単な $b$ を使って $B$ を求めよう。正弦定理より
1組の向かい合う角の大きさと辺の長さが分かったから,正弦定理を利用して残りの角の大きさを求めよう。
ABの長さは $c=\sqrt{3}+1$ で少し複雑なので,より簡単な $b$ を使って $B$ を求めよう。正弦定理より
\begin{align*}
&\dfrac{b}{\sin B}=\dfrac{a}{\sin A} \\[4pt]
&\sin B=\dfrac{b}{a}\sin A
\end{align*}
となるから&\dfrac{b}{\sin B}=\dfrac{a}{\sin A} \\[4pt]
&\sin B=\dfrac{b}{a}\sin A
\end{align*}
\begin{align*}
\sin B&=\dfrac{2}{\sqrt{2}}\sin 30\Deg \\[4pt]
&=\dfrac{2}{\sqrt{2}}\Cdota\dfrac{1}{2}=\dfrac{1}{\sqrt{2}}
\end{align*}
$0\Deg<b<180\Deg$ であるから,$B=45\Deg,~135\Deg$ コサインの場合と異なり,サインの値からは角が1つに決まらない。今回は与えられている条件が三角形の合同条件の1つである「2辺とその間の角」であるため,求めた2つの角度のうち,どちらか一方のみが条件をみたすはずである。 したがって,どちらが条件を満たすのかを調べる必要がある。その方法としては辺と角の大小関係に着目するのが有効である。 $a=\sqrt{2},~b=2,~c=\sqrt{3}+1$ より,$a<b<c$ であるから,$A<B<C$ となり $B$ は鋭角であることが分かる。よって,$B=45\Deg$ となる。 最後の角 $C$ は三角形の内角の和が180°であることから簡単に求めることができる。\sin B&=\dfrac{2}{\sqrt{2}}\sin 30\Deg \\[4pt]
&=\dfrac{2}{\sqrt{2}}\Cdota\dfrac{1}{2}=\dfrac{1}{\sqrt{2}}
\end{align*}