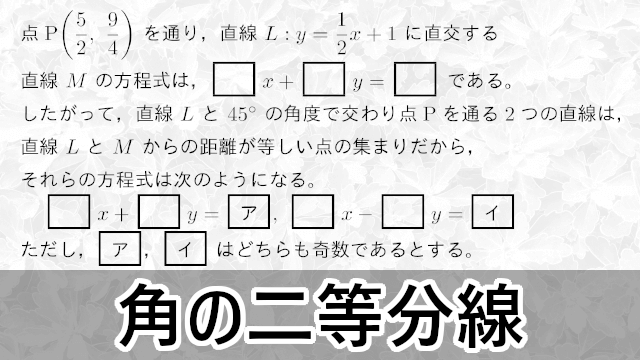
ここでは,角の二等分線の方程式について説明します。
ある角を等しい角に分ける直線が角の二等分線だということは分かっているかもしれませんが,いざ「その方程式を求めよ」と言われると,どうするのか分からない・・・となってしまう人が少なくなりません。
定義だけでなく性質についてもしっかり理解しておいたほうが良いでしょう。
Contents
角の二等分線とは

ヒロ
角の二等分線の定義は次のようになっている。
角の二等分線$\kaku{AOB}$ を等しい角度に2つに分ける直線を $\kaku{AOB}$ の二等分線という。
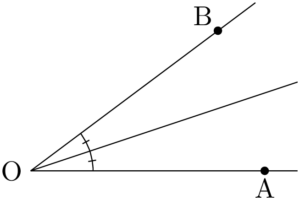


ヒロ
大学入試問題を解く際には,この定義以外に「角の二等分線の性質」を知っておくと良いだろう。
角の二等分線の性質$\kaku{AOB}$ の二等分線上の任意の点から,2直線OA,OBまでの距離は等しい。
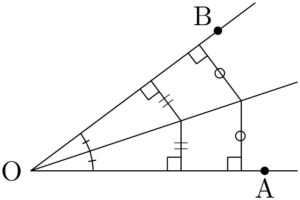


ヒロ
サクッと証明しておこう。
【証明】
$\kaku{AOB}$ の二等分線上の点Pから,2つの半直線OAとOBに下ろした垂線の足をそれぞれC,Dとする。2つの三角形 $\sankaku{OPC}$ と $\sankaku{OPD}$ は,ともに直角三角形で斜辺と1つの鋭角がそれぞれ等しいから合同である。
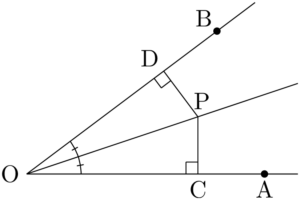
したがって,対応する辺の長さは等しいから,$\text{PC}=\text{PD}$ である。つまり,$\kaku{AOB}$ の二等分線上の任意の点から,2直線OA,OBまでの距離は等しい。
$\kaku{AOB}$ の二等分線上の点Pから,2つの半直線OAとOBに下ろした垂線の足をそれぞれC,Dとする。2つの三角形 $\sankaku{OPC}$ と $\sankaku{OPD}$ は,ともに直角三角形で斜辺と1つの鋭角がそれぞれ等しいから合同である。

したがって,対応する辺の長さは等しいから,$\text{PC}=\text{PD}$ である。つまり,$\kaku{AOB}$ の二等分線上の任意の点から,2直線OA,OBまでの距離は等しい。

ヒロ
「三角形の内角の二等分線の長さ」で説明したように,角の二等分線の長さに関する性質・公式もついでに復習しておくと良いだろう。