2020年センター試験 数学ⅠA 第1問 二次関数の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2020年 センターⅠA 第1問 二次関数 $c$ を定数とする。2次関数 $y=x^2$ のグラフを,2点 $(c,~0)$, $(c+4,~0)$ を通るように平行移動して得られるグラフを $G$ とする。
(1) $G$ をグラフにもつ2次関数は,$c$ を用いて
2点 $(3,~0)$, $(3,~-3)$ を両端とする線分と $G$ が共有点をもつような $c$ の値の範囲は
(2) $\mybox{ニ}\leqq c\leqq\mybox{ヌ}$ の場合を考える。$G$ が点 $(3,~-1)$ を通るとき,$G$ は2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\myBox{ネ}+\sqrt{\myBox{ノ}}$,$y$ 軸方向に $\myBox{ハヒ}$ だけ平行移動したものである。また,このとき $G$ と $y$ 軸との交点の $y$ 座標は $\myBox{フ}+\myBox{ヘ}\sqrt{\myBox{ホ}}$ である。
(1) $G$ をグラフにもつ2次関数は,$c$ を用いて
\begin{align*}
y=x^2-2\left(c+\myBox{ツ}\right)x+c\left(c+\myBox{テ}\right)
\end{align*}
と表せる。y=x^2-2\left(c+\myBox{ツ}\right)x+c\left(c+\myBox{テ}\right)
\end{align*}
2点 $(3,~0)$, $(3,~-3)$ を両端とする線分と $G$ が共有点をもつような $c$ の値の範囲は
\begin{align*}
-\myBox{ト}\leqq c\leqq\myBox{ナ},~\myBox{ニ}\leqq c\leqq\myBox{ヌ}
\end{align*}
である。-\myBox{ト}\leqq c\leqq\myBox{ナ},~\myBox{ニ}\leqq c\leqq\myBox{ヌ}
\end{align*}
(2) $\mybox{ニ}\leqq c\leqq\mybox{ヌ}$ の場合を考える。$G$ が点 $(3,~-1)$ を通るとき,$G$ は2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\myBox{ネ}+\sqrt{\myBox{ノ}}$,$y$ 軸方向に $\myBox{ハヒ}$ だけ平行移動したものである。また,このとき $G$ と $y$ 軸との交点の $y$ 座標は $\myBox{フ}+\myBox{ヘ}\sqrt{\myBox{ホ}}$ である。
(1)の考え方と解答

ヒロ
通る2点の座標と $x^2$ の係数から頂点の座標をサクッと求めてしまおう。
【ツテの解答】
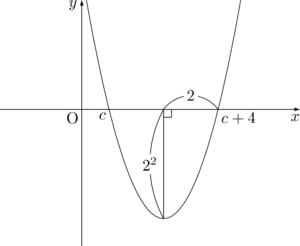
2点 $(c,~0)$, $(c+4,~0)$ を通るグラフ $G$ の頂点の $x$ 座標は $c+2$ である。
また,グラフ $G$ が $x$ 軸から切り取る線分の長さが4であるから,2乗に比例する性質を利用すると,頂点の $y$ 座標は $-4$ であることが分かる。
よって,求める2次関数は
2点 $(c,~0)$, $(c+4,~0)$ を通るグラフ $G$ の頂点の $x$ 座標は $c+2$ である。
また,グラフ $G$ が $x$ 軸から切り取る線分の長さが4であるから,2乗に比例する性質を利用すると,頂点の $y$ 座標は $-4$ であることが分かる。

よって,求める2次関数は
\begin{align*}
y&=\{x-(c+2)\}^2-4 \\[4pt]&=x^2-2(c+2)x+(c+2)^2-4 \\[4pt]&=x^2-2(c+2)x+c(c+4)
\end{align*}
y&=\{x-(c+2)\}^2-4 \\[4pt]&=x^2-2(c+2)x+(c+2)^2-4 \\[4pt]&=x^2-2(c+2)x+c(c+4)
\end{align*}

ヒロ
次は $y$ 軸に平行な線分とグラフ $G$ が共有点をもつ条件を求める問題。
【ト~ヌの解答】
条件を満たすのは,$x=3$ のときの $y$ が $-3$ 以上0以下の範囲になるときだから
条件を満たすのは,$x=3$ のときの $y$ が $-3$ 以上0以下の範囲になるときだから
\begin{align*}
&-3\leqq\{3-(c+2)\}^2-4\leqq0 \\[4pt]&1\leqq(c-1)^2\leqq4 \\[4pt]&-2\leqq c-1\leqq-1,~1\leqq c-1\leqq2 \\[4pt]&-1\leqq c\leqq0,~2\leqq c\leqq3
\end{align*}
&-3\leqq\{3-(c+2)\}^2-4\leqq0 \\[4pt]&1\leqq(c-1)^2\leqq4 \\[4pt]&-2\leqq c-1\leqq-1,~1\leqq c-1\leqq2 \\[4pt]&-1\leqq c\leqq0,~2\leqq c\leqq3
\end{align*}

ヒロ
$c$ が一か所に集まっている平方完成された式を利用するのが楽だね。
(2)の考え方と解答
(2) $\mybox{ニ}\leqq c\leqq\mybox{ヌ}$ の場合を考える。$G$ が点 $(3,~-1)$ を通るとき,$G$ は2次関数 $y=x^2$ のグラフを $x$ 軸方向に $\myBox{ネ}+\sqrt{\myBox{ノ}}$,$y$ 軸方向に $\myBox{ハヒ}$ だけ平行移動したものである。また,このとき $G$ と $y$ 軸との交点の $y$ 座標は $\myBox{フ}+\myBox{ヘ}\sqrt{\myBox{ホ}}$ である。

ヒロ
グラフ $G$ が点 $(3,~-1)$ を通るときの $c$ の値を求めれば,頂点の座標も分かるから,平行移動量も分かるね。
【ネ~ヒの解答】
$G$ が点 $(3,~-1)$ を通るとき
頂点の座標を $(p,~q)$ とすると
$G$ が点 $(3,~-1)$ を通るとき
\begin{align*}
&\{3-(c+2)\}^2-4=-1 \\[4pt]&(c-1)^2=3 \\[4pt]&c=1\pm\sqrt{3}
\end{align*}
$2\leqq c\leqq3$ より $c=1+\sqrt{3}$&\{3-(c+2)\}^2-4=-1 \\[4pt]&(c-1)^2=3 \\[4pt]&c=1\pm\sqrt{3}
\end{align*}
頂点の座標を $(p,~q)$ とすると
\begin{align*}
&p=c+2=3+\sqrt{3} \\[4pt]&q=-4
\end{align*}
であるから,$G$ は2次関数 $y=x^2$ のグラフを $x$ 軸方向に $3+\sqrt{3}$,$y$ 軸方向に $-4$ だけ平行移動したものである。&p=c+2=3+\sqrt{3} \\[4pt]&q=-4
\end{align*}

ヒロ
最後は $G$ と $y$ 軸の交点の $y$ 座標を求める問題。
【フ~ホの解答】
求める値は $x=0$ のときの $y$ の値,すなわち $G$ の式の定数項だから
\begin{align*} c(c+4)&=(1+\sqrt{3})(5+\sqrt{3}) \\[4pt] &=5+6\sqrt{3}+3 \\[4pt] &=8+6\sqrt{3} \end{align*}

ヒロ
2乗に比例する性質を利用して解くと次のようになる。
【フ~ホの別解】
$y$ 軸と軸の距離が $3+\sqrt{3}$ だから,2乗に比例する性質を利用すると,求める $y$ 座標は次のようになる。
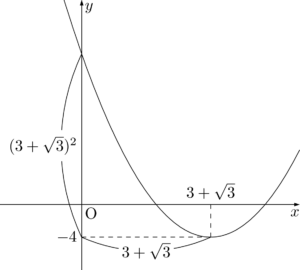
\begin{align*} &-4+(3+\sqrt{3})^2 \\[4pt] &=-4+12+6\sqrt{3} \\[4pt] &=8+6\sqrt{3} \end{align*}

2020年 センター数学ⅠA 二次関数を解いた感想

ヒロ
2次関数のグラフがもつ「2乗に比例する性質」がポイントとなる。

ヒロ
2乗に比例する性質を使いこなすことができれば,かなり計算量を少なくすることができるため,時間短縮をすることができる。





















