Contents
角の二等分線の方程式の求め方

ヒロ
角の二等分線の方程式を求める方法を説明する。
【角の二等分線の方程式】
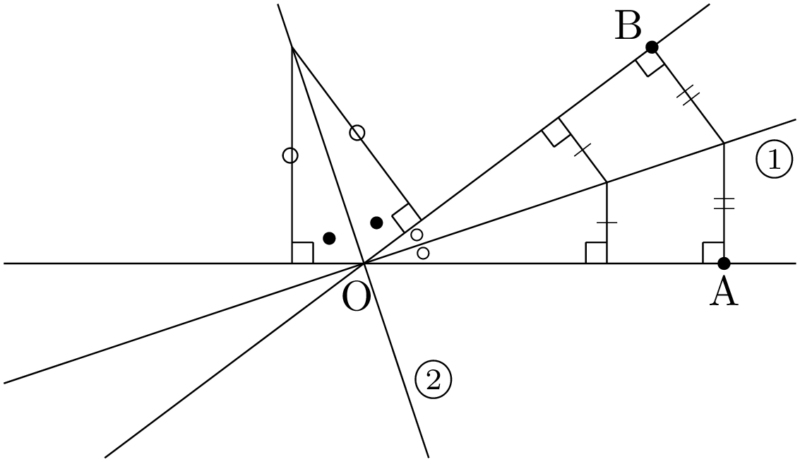
2つの半直線OA,OBの角の二等分線上の点をP$(X,~Y)$ とし,2直線OA,OBの方程式をそれぞれ
\begin{align*}
ax+by+c=0,~px+qy+r=0
\end{align*}
とする。点Pから半直線OA,OBまでの距離が等しいからax+by+c=0,~px+qy+r=0
\end{align*}
\begin{align*}
\dfrac{\abs{aX+bY+c}}{\sqrt{a^2+b^2}}=\dfrac{\abs{pX+qY+r}}{\sqrt{p^2+q^2}}
\end{align*}
これを変形して\dfrac{\abs{aX+bY+c}}{\sqrt{a^2+b^2}}=\dfrac{\abs{pX+qY+r}}{\sqrt{p^2+q^2}}
\end{align*}
\begin{align*}
kX+lY+m=0,~k’X+l’Y+m’=0
\end{align*}
となったとすると,求める角の二等分線の方程式はkX+lY+m=0,~k’X+l’Y+m’=0
\end{align*}
\begin{align*}
kx+ly+m=0,~k’x+l’y+m’=0
\end{align*}
である。ここで2本の直線となるのは,外角の二等分線の方程式も求めているからである。つまり,$\kaku{AOB}$ の二等分線といえば直線①を表すが,上の計算では直線②も得られることになる。kx+ly+m=0,~k’x+l’y+m’=0
\end{align*}
問題によっては「2直線OA,OBのなす角を二等分する直線の方程式を求めよ。」となることもあり,この場合は,①と②の2直線の方程式を求めればよい。
いずれにしても,2本の直線が求まってしまって,驚かないようにしておくことが重要である。
絶対値を含む等式の変形

ヒロ
2直線までの距離が等しいことを利用して角の二等分線の方程式を求める場合,絶対値を含む等式の変形をすることになる。

ヒロ
変形の基本を知っておこう。
絶対値を含む等式の変形$\abs{a}=\abs{b}$ は $a=b$ または $a=-b$ と同値である。

ヒロ
簡単に説明しておく。
【絶対値を含む等式の変形】
$\abs{a}=\abs{b}$ が成り立つとき,両辺の絶対値の中身の符号に着目すると4つの場合に分けられる。1つずつ説明していく。
(i) $a\geqq0,~b\geqq0$ のとき
$\abs{a}=a,~\abs{b}=b$ であるから,$\abs{a}=\abs{b}$ は $a=b$ となる。
(ii) $a\geqq0,~b\leqq0$ のとき
$\abs{a}=a,~\abs{b}=-b$ であるから,$\abs{a}=\abs{b}$ は $a=-b$ となる。
(iii) $a\leqq0,~b\geqq0$ のとき
$\abs{a}=-a,~\abs{b}=b$ であるから,$\abs{a}=\abs{b}$ は $-a=b$,すなわち $a=-b$ となる。
(iv) $a\leqq0,~b\leqq0$ のとき
$\abs{a}=-a,~\abs{b}=-b$ であるから,$\abs{a}=\abs{b}$ は $-a=-b$,すなわち $a=b$ となる。
(i)~(iv)から,$\abs{a}=\abs{b}$ は $a=b$ または $a=-b$ と同値であることが分かる。

ヒロ
このことはよく利用するので,素早く変形できるようにしておこう。