ここでは角の二等分線の長さについて説明します。
大学入試問題では,角の二等分線の長さに関する問題が出題されることがあります。
基本的な解法はもちろん,裏技的解法も身に付けましょう。
角の二等分線の長さを求める問題
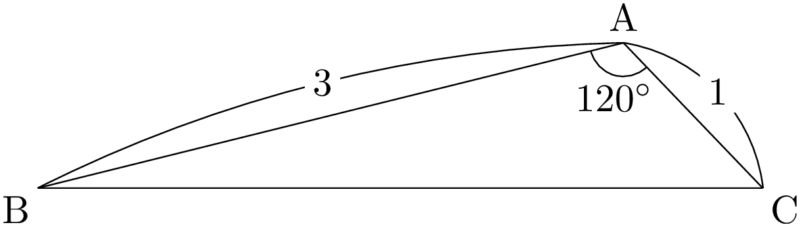
問題$\kaku{A}=120\Deg$, $\text{AB}=3$, $\text{AC}=1$ である $\sankaku{ABC}$ の $\kaku{A}$ の二等分線が辺BCと交わる点をDとするとき,線分ADの長さを求めよ。
【考え方と解答】
$\sankaku{ABC}$ は次のようになっている。
角の二等分線を引くと次のようになる。
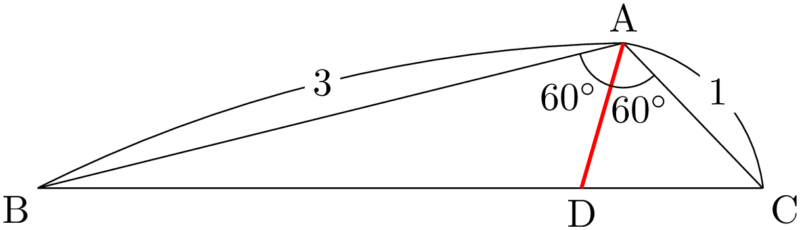
$\text{AD}$ の長さを求めるために,ADを含む三角形を探すと $\sankaku{ABD}$ と $\sankaku{ACD}$ が見つかる。$\sankaku{ABC}$ の面積を求めることができることを利用して,ADの長さを求めよう。
$\sankaku{ABC}$ は次のようになっている。

角の二等分線を引くと次のようになる。

$\text{AD}$ の長さを求めるために,ADを含む三角形を探すと $\sankaku{ABD}$ と $\sankaku{ACD}$ が見つかる。$\sankaku{ABC}$ の面積を求めることができることを利用して,ADの長さを求めよう。
\begin{align*}
&\sankaku{ABC}=\sankaku{ABD}+\sankaku{ACD} \\[4pt]
&\dfrac{1}{2}\text{AB}\Cdota\text{AC}\sin120\Deg=\dfrac{1}{2}\text{AB}\Cdota\text{AD}\sin60\Deg+\dfrac{1}{2}\text{AC}\Cdota\text{AD}\sin60\Deg \\[4pt]
&3\Cdota1\Cdota\dfrac{\sqrt{3}}{2}=3\text{AD}\Cdota\dfrac{\sqrt{3}}{2}+\text{AD}\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&4\text{AD}=3 \\[4pt]
&\text{AD}=\dfrac{3}{4}
\end{align*}
&\sankaku{ABC}=\sankaku{ABD}+\sankaku{ACD} \\[4pt]
&\dfrac{1}{2}\text{AB}\Cdota\text{AC}\sin120\Deg=\dfrac{1}{2}\text{AB}\Cdota\text{AD}\sin60\Deg+\dfrac{1}{2}\text{AC}\Cdota\text{AD}\sin60\Deg \\[4pt]
&3\Cdota1\Cdota\dfrac{\sqrt{3}}{2}=3\text{AD}\Cdota\dfrac{\sqrt{3}}{2}+\text{AD}\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&4\text{AD}=3 \\[4pt]
&\text{AD}=\dfrac{3}{4}
\end{align*}

ヒロ
他の方法でADの長さを求めることもできる。
【別の考え方と解答】
角の二等分線の性質から,$\text{BD}:\text{DC}=3:1$ となる。
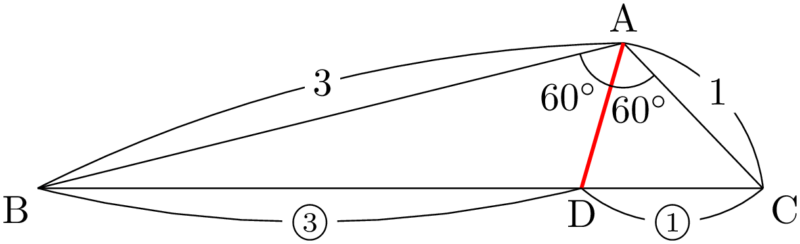
BCの長さを求めることで,BDやCDの長さも求めることができる。実際に求めてみよう。
$\sankaku{ABC}$ において,余弦定理より
$\text{BD}:\text{DC}=3:1$ であるから
角の二等分線の性質から,$\text{BD}:\text{DC}=3:1$ となる。

BCの長さを求めることで,BDやCDの長さも求めることができる。実際に求めてみよう。
$\sankaku{ABC}$ において,余弦定理より
\begin{align*}
\text{BC}^2&=3^2+1^2-2\Cdota3\Cdota1\cos120\Deg \\[4pt]
&=9+1-6\Cdota\left(-\dfrac{1}{2}\right)=13
\end{align*}
$\text{BC}>0$ より $\text{BC}=\sqrt{13}$\text{BC}^2&=3^2+1^2-2\Cdota3\Cdota1\cos120\Deg \\[4pt]
&=9+1-6\Cdota\left(-\dfrac{1}{2}\right)=13
\end{align*}
$\text{BD}:\text{DC}=3:1$ であるから
\begin{align*}
\text{BD}=\dfrac{3}{4}\text{BC}=\dfrac{3\sqrt{13}}{4}
\end{align*}
$\sankaku{ABC}$ において余弦定理を適用して $\cos B$ を求めてADを求めることにする。\text{BD}=\dfrac{3}{4}\text{BC}=\dfrac{3\sqrt{13}}{4}
\end{align*}
\begin{align*}
\cos B&=\dfrac{3^2+(\sqrt{13})^2-1^2}{2\Cdot3\Cdot\sqrt{13}} \\[4pt]
&=\dfrac{21}{2\Cdot3\Cdot\sqrt{13}}=\dfrac{7}{2\sqrt{13}}
\end{align*}
$\sankaku{ABD}$ において,余弦定理より\cos B&=\dfrac{3^2+(\sqrt{13})^2-1^2}{2\Cdot3\Cdot\sqrt{13}} \\[4pt]
&=\dfrac{21}{2\Cdot3\Cdot\sqrt{13}}=\dfrac{7}{2\sqrt{13}}
\end{align*}
\begin{align*}
\text{AD}^2&=3^2+\left(\dfrac{3\sqrt{13}}{4}\right)^2-2\Cdota3\Cdota\dfrac{3\sqrt{13}}{4}\Cdota\dfrac{7}{2\sqrt{13}} \\[4pt]
&=9+\dfrac{117}{16}-\dfrac{63}{4} \\[4pt]
&=\dfrac{144+117-252}{16}=\dfrac{9}{16}
\end{align*}
$\text{AD}>0$ より $\text{AD}=\dfrac{3}{4}$\text{AD}^2&=3^2+\left(\dfrac{3\sqrt{13}}{4}\right)^2-2\Cdota3\Cdota\dfrac{3\sqrt{13}}{4}\Cdota\dfrac{7}{2\sqrt{13}} \\[4pt]
&=9+\dfrac{117}{16}-\dfrac{63}{4} \\[4pt]
&=\dfrac{144+117-252}{16}=\dfrac{9}{16}
\end{align*}

ヒロ
$\text{BD}^2=$ で始まる形で余弦定理を使った場合にどうなるかを説明しておく。
【余弦定理の使い方を変えた場合】
$\sankaku{ABD}$ において余弦定理を適用すると
「$\text{AB}=3,~\text{BD}=\dfrac{3\sqrt{13}}{4},~\kaku{BAD}=60\Deg$」は三角形の合同条件ではないため,ADの長さが1つに決まらない。$\text{AD}=\dfrac{9}{4}$ となる点Aの場所を図示すると,次の図の $\text{A}’$ になる。
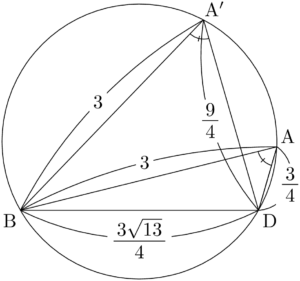
得られた値が $\dfrac{9}{4}$ で正であるから,本来の解でないことを示すことが少し面倒である。
$\kaku{ADB}$ が鈍角であることを利用すると,次のように $\dfrac{9}{4}$ が不適であることを示すことができる。
$\text{AD}=\dfrac{9}{4}$ のとき
これで $\text{AD}=\dfrac{3}{4}$ となる。
$\sankaku{ABD}$ において余弦定理を適用すると
\begin{align*}
&\left(\dfrac{3\sqrt{13}}{4}\right)^2=3^2+\text{AD}^2-2\Cdota3\text{AD}\cos60\Deg \\[4pt]
&\dfrac{117}{16}=9+\text{AD}^2-3\text{AD} \\[4pt]
&16\text{AD}^2-48\text{AD}+27=0 \\[4pt]
&(4\text{AD}-3)(4\text{AD}-9)=0 \\[4pt]
&\text{AD}=\dfrac{3}{4},~\dfrac{9}{4}
\end{align*}
本来の解 $\dfrac{3}{4}$ とは異なる解 $\dfrac{9}{4}$ が得られる。&\left(\dfrac{3\sqrt{13}}{4}\right)^2=3^2+\text{AD}^2-2\Cdota3\text{AD}\cos60\Deg \\[4pt]
&\dfrac{117}{16}=9+\text{AD}^2-3\text{AD} \\[4pt]
&16\text{AD}^2-48\text{AD}+27=0 \\[4pt]
&(4\text{AD}-3)(4\text{AD}-9)=0 \\[4pt]
&\text{AD}=\dfrac{3}{4},~\dfrac{9}{4}
\end{align*}
「$\text{AB}=3,~\text{BD}=\dfrac{3\sqrt{13}}{4},~\kaku{BAD}=60\Deg$」は三角形の合同条件ではないため,ADの長さが1つに決まらない。$\text{AD}=\dfrac{9}{4}$ となる点Aの場所を図示すると,次の図の $\text{A}’$ になる。

得られた値が $\dfrac{9}{4}$ で正であるから,本来の解でないことを示すことが少し面倒である。
$\kaku{ADB}$ が鈍角であることを利用すると,次のように $\dfrac{9}{4}$ が不適であることを示すことができる。
$\text{AD}=\dfrac{9}{4}$ のとき
\begin{align*}
&\left(\dfrac{9}{4}\right)^2+\left(\dfrac{3\sqrt{13}}{4}\right)^2-3^2 \\[4pt]
&=\dfrac{81+117-144}{16}=\dfrac{54}{16}=\dfrac{27}{8}>0
\end{align*}
であるから $\kaku{ADB}$ が鋭角となるから不適。&\left(\dfrac{9}{4}\right)^2+\left(\dfrac{3\sqrt{13}}{4}\right)^2-3^2 \\[4pt]
&=\dfrac{81+117-144}{16}=\dfrac{54}{16}=\dfrac{27}{8}>0
\end{align*}
これで $\text{AD}=\dfrac{3}{4}$ となる。
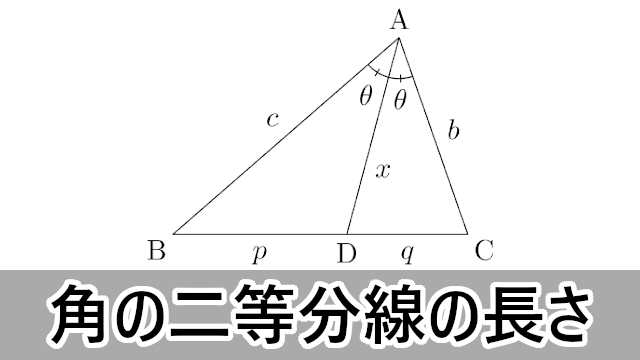
角の二等分線の長さに関する性質

ヒロ
まず,角の二等分線の長さに関する性質をまとめておく。
角の二等分線の長さの性質
$\sankaku{ABC}$ の $A$ の二等分線と辺BCの交点をDとする。
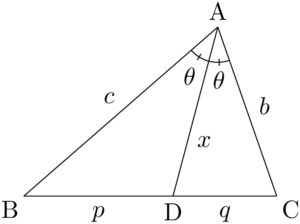

- $c:b=p:q$
- $x=\dfrac{bc\sin2\theta}{(b+c)\sin\theta}=\dfrac{2bc\cos\theta}{b+c}$
- $x=\sqrt{bc-pq}$

ヒロ
これらの性質を証明しておく。
【性質1の証明】
点Cを通りADと平行な直線と直線ABとの交点をEとする。
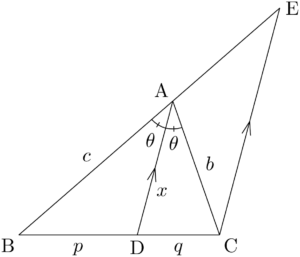
DAとCEが平行であり,同位角・錯角が等しいから
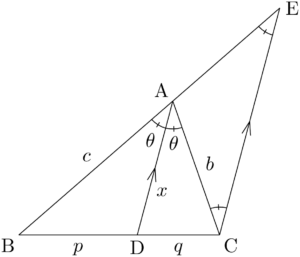
$\sankaku{ACE}$ の底角が等しいから $\sankaku{ACE}$ は二等辺三角形であり,$\text{AC}=\text{AE}$ である。
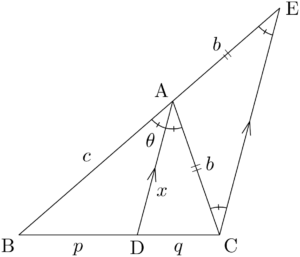
$\text{BA}:\text{AE}=\text{BD}:\text{DC}$ より
点Cを通りADと平行な直線と直線ABとの交点をEとする。

DAとCEが平行であり,同位角・錯角が等しいから
\begin{align*}
\kaku{ACE}=\kaku{AEC}=\theta
\end{align*}
である。\kaku{ACE}=\kaku{AEC}=\theta
\end{align*}

$\sankaku{ACE}$ の底角が等しいから $\sankaku{ACE}$ は二等辺三角形であり,$\text{AC}=\text{AE}$ である。

$\text{BA}:\text{AE}=\text{BD}:\text{DC}$ より
\begin{align*}
c:b=p:q
\end{align*}
c:b=p:q
\end{align*}
【性質2の証明】
$\sankaku{ABD}+\sankaku{ACD}=\sankaku{ABC}$ より
$\sankaku{ABD}+\sankaku{ACD}=\sankaku{ABC}$ より
\begin{align*}
&\dfrac{1}{2}cx\sin\theta+\dfrac{1}{2}bx\sin\theta=\dfrac{1}{2}bc\sin2\theta \\[4pt]
&(b+c)x\sin\theta=bc\sin2\theta \\[4pt]
&x=\dfrac{bc\sin2\theta}{(b+c)\sin\theta}
\end{align*}
数学Ⅱの三角関数で学ぶ2倍角の公式「$\sin2\theta=2\sin\theta\cos\theta$」を利用すると,&\dfrac{1}{2}cx\sin\theta+\dfrac{1}{2}bx\sin\theta=\dfrac{1}{2}bc\sin2\theta \\[4pt]
&(b+c)x\sin\theta=bc\sin2\theta \\[4pt]
&x=\dfrac{bc\sin2\theta}{(b+c)\sin\theta}
\end{align*}
\begin{align*}
x&=\dfrac{bc\sin2\theta}{(b+c)\sin\theta} \\[4pt]
&=\dfrac{2bc\sin\theta\cos\theta}{(b+c)\sin\theta} \\[4pt]
&=\dfrac{2bc\cos\theta}{b+c}
\end{align*}
x&=\dfrac{bc\sin2\theta}{(b+c)\sin\theta} \\[4pt]
&=\dfrac{2bc\sin\theta\cos\theta}{(b+c)\sin\theta} \\[4pt]
&=\dfrac{2bc\cos\theta}{b+c}
\end{align*}

ヒロ
三角形の相似を利用して,性質3を証明すると次のようになる。
【性質3の証明】
直線ADと三角形ABCの外接円の交点のうち,Aと異なる点をEとする。
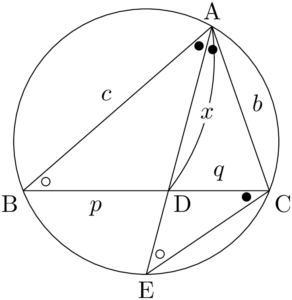
$\ko{\text{AC}}$ に対する円周角に着目すると
直線ADと三角形ABCの外接円の交点のうち,Aと異なる点をEとする。

$\ko{\text{AC}}$ に対する円周角に着目すると
\begin{align*}
\kaku{CBA}=\kaku{AEC}
\end{align*}
である。したがって,$\sankaku{ABD}$∽$\sankaku{AEC}$ であることが分かるから\kaku{CBA}=\kaku{AEC}
\end{align*}
\begin{align*}
&\text{AB}:\text{AE}=\text{AD}:\text{AC} \\[4pt]
&\text{AE}\Cdota\text{AD}=\text{AC}\Cdota\text{AB} \\[4pt]
&x\text{AE}=bc~\cdots\cdots①
\end{align*}
また $\ko{\text{BE}}$ に対する円周角より,$\kaku{BAD}=\kaku{BCE}$ であるから,$\sankaku{ABD}$∽$\sankaku{CED}$ である。よって&\text{AB}:\text{AE}=\text{AD}:\text{AC} \\[4pt]
&\text{AE}\Cdota\text{AD}=\text{AC}\Cdota\text{AB} \\[4pt]
&x\text{AE}=bc~\cdots\cdots①
\end{align*}
\begin{align*}
&\text{AD}:\text{CD}=\text{BD}:\text{ED} \\[4pt]
&\text{AD}\Cdota\text{ED}=\text{BD}\Cdota\text{CD} \\[4pt]
&x\text{DE}=pq~\cdots\cdots②
\end{align*}
$①-②$ より&\text{AD}:\text{CD}=\text{BD}:\text{ED} \\[4pt]
&\text{AD}\Cdota\text{ED}=\text{BD}\Cdota\text{CD} \\[4pt]
&x\text{DE}=pq~\cdots\cdots②
\end{align*}
\begin{align*}
&x(\text{AE}-\text{DE})=bc-pq \\[4pt]
&x\text{AD}=bc-pq \\[4pt]
&x^2=bc-pq
\end{align*}
$x>0$ より,$x=\sqrt{bc-pq}$&x(\text{AE}-\text{DE})=bc-pq \\[4pt]
&x\text{AD}=bc-pq \\[4pt]
&x^2=bc-pq
\end{align*}

ヒロ
余弦定理を利用すると次のように証明することができる。
【性質3の証明2】
(i) $b=c$ のとき,$\sankaku{ABC}$ は二等辺三角形であるから $p=q$ となり,ADとBCは垂直になる。このとき $\sankaku{ABD}$ に着目すると
(ii) $b\neq c$ のとき,$\sankaku{ABD}$ において,余弦定理より
(i) $b=c$ のとき,$\sankaku{ABC}$ は二等辺三角形であるから $p=q$ となり,ADとBCは垂直になる。このとき $\sankaku{ABD}$ に着目すると
\begin{align*}
x=\sqrt{c^2-p^2}
\end{align*}
である。また,$\sankaku{ACD}$ に着目してもx=\sqrt{c^2-p^2}
\end{align*}
\begin{align*}
x=\sqrt{b^2-q^2}
\end{align*}
であるから,$x=\sqrt{bc-pq}$ が成り立つ。x=\sqrt{b^2-q^2}
\end{align*}
(ii) $b\neq c$ のとき,$\sankaku{ABD}$ において,余弦定理より
\begin{align*}
&p^2=c^2+x^2-2cx\cos\theta \\[4pt]
&\cos\theta=\dfrac{x^2+c^2-p^2}{2cx}
\end{align*}
$\sankaku{ACD}$ において,余弦定理より&p^2=c^2+x^2-2cx\cos\theta \\[4pt]
&\cos\theta=\dfrac{x^2+c^2-p^2}{2cx}
\end{align*}
\begin{align*}
&q^2=b^2+x^2-2bx\cos\theta \\[4pt]
&\cos\theta=\dfrac{x^2+b^2-q^2}{2bx}
\end{align*}
よって&q^2=b^2+x^2-2bx\cos\theta \\[4pt]
&\cos\theta=\dfrac{x^2+b^2-q^2}{2bx}
\end{align*}
\begin{align*}
&\dfrac{x^2+c^2-p^2}{2cx}=\dfrac{x^2+b^2-q^2}{2bx} \\[4pt]
&b(x^2+c^2-p^2)=c(x^2+b^2-q^2) \\[4pt]
&(b-c)x^2=bc(b-c)+bp^2-cq^2
\end{align*}
ここで,性質1より $bp=cq$ が成り立つから&\dfrac{x^2+c^2-p^2}{2cx}=\dfrac{x^2+b^2-q^2}{2bx} \\[4pt]
&b(x^2+c^2-p^2)=c(x^2+b^2-q^2) \\[4pt]
&(b-c)x^2=bc(b-c)+bp^2-cq^2
\end{align*}
\begin{align*}
&(b-c)x^2=bc(b-c)+cpq-bpq \\[4pt]
&(b-c)x^2=bc(b-c)-pq(b-c)
\end{align*}
$b\neq c$ であるから&(b-c)x^2=bc(b-c)+cpq-bpq \\[4pt]
&(b-c)x^2=bc(b-c)-pq(b-c)
\end{align*}
\begin{align*}
&x^2=bc-pq
\end{align*}
$x>0$ より,$x=\sqrt{bc-pq}$&x^2=bc-pq
\end{align*}

ヒロ
$\kaku{ADB}$ に着目すると場合分けをする必要がなくなる。
【性質3の証明3】
性質1より,$c:b=p:q$ であるから,
性質1より,$c:b=p:q$ であるから,
\begin{align*}
p=\dfrac{ca}{b+c},~q=\dfrac{ba}{b+c}
\end{align*}
また,$\kaku{ADB}=\alpha$ とすると $\sankaku{ABD}$ と $\sankaku{ACD}$ において,余弦定理よりp=\dfrac{ca}{b+c},~q=\dfrac{ba}{b+c}
\end{align*}
\begin{align*}
&c^2=x^2+p^2-2px\cos\alpha~\cdots\cdots① \\[4pt]
&b^2=x^2+q^2-2qx\cos(180\Deg-\alpha) \\[4pt]
&b^2=x^2+q^2+2qx\cos\alpha~\cdots\cdots②
\end{align*}
$①\times q+②\times p$ より&c^2=x^2+p^2-2px\cos\alpha~\cdots\cdots① \\[4pt]
&b^2=x^2+q^2-2qx\cos(180\Deg-\alpha) \\[4pt]
&b^2=x^2+q^2+2qx\cos\alpha~\cdots\cdots②
\end{align*}
\begin{align*}
&c^2q+b^2p=(q+p)x^2+p^2q+pq^2 \\[4pt]
&(p+q)x^2=\dfrac{c^2ba}{b+c}+\dfrac{b^2ca}{b+c}-pq(p+q) \\[4pt]
&ax^2=\dfrac{abc(c+b)}{b+c}-apq \\[4pt]
&ax^2=a(bc-pq)
\end{align*}
両辺を $a$ で割って&c^2q+b^2p=(q+p)x^2+p^2q+pq^2 \\[4pt]
&(p+q)x^2=\dfrac{c^2ba}{b+c}+\dfrac{b^2ca}{b+c}-pq(p+q) \\[4pt]
&ax^2=\dfrac{abc(c+b)}{b+c}-apq \\[4pt]
&ax^2=a(bc-pq)
\end{align*}
\begin{align*}
x^2=bc-pq
\end{align*}
$x>0$ より,$x=\sqrt{bc-pq}$x^2=bc-pq
\end{align*}

ヒロ
性質2や性質3を覚えてうまく使うことで,答えだけを書けば良い形式の試験やマーク式試験においては時間短縮することができる。
角の二等分線の長さの性質の利用

ヒロ
最初に解いた問題をもう一度解いてみよう。
$\kaku{A}=120\Deg$, $\text{AB}=3$, $\text{AC}=1$ である $\sankaku{ABC}$ の $\kaku{A}$ の二等分線が辺BCと交わる点をDとするとき,線分ADの長さを求めよ。
【性質2を利用した解法】

与えられた2辺の間の角が $120\Deg$ であるから,性質2に $\theta=60\Deg$ を代入すると

したがって,

与えられた2辺の間の角が $120\Deg$ であるから,性質2に $\theta=60\Deg$ を代入すると
\begin{align*}
x=\dfrac{bc}{b+c}
\end{align*}
となる。x=\dfrac{bc}{b+c}
\end{align*}

したがって,
\begin{align*}
\text{AD}=\dfrac{3\Cdot1}{3+1}=\dfrac{3}{4}
\end{align*}
\text{AD}=\dfrac{3\Cdot1}{3+1}=\dfrac{3}{4}
\end{align*}
【性質3を利用した解法】
$\sankaku{ABC}$ において,余弦定理より
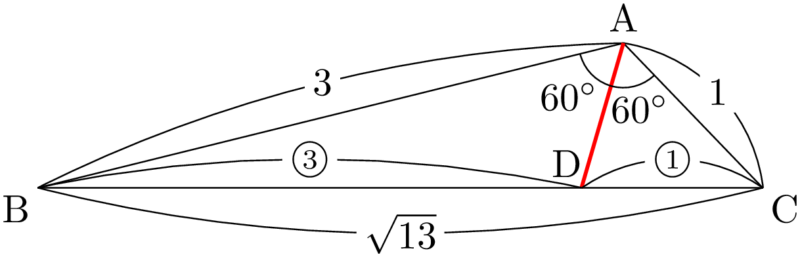
$\text{BD}:\text{DC}=3:1$ であるから
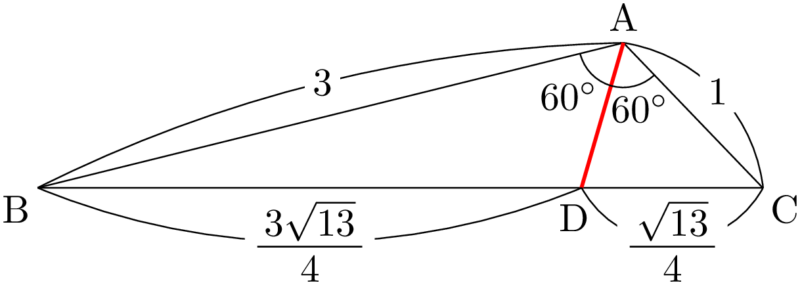
性質3より
$\sankaku{ABC}$ において,余弦定理より
\begin{align*}
\text{BC}^2&=3^2+1^2-2\Cdota3\Cdota1\cos120\Deg \\[4pt]
&=10+3=13
\end{align*}
よって,$\text{BC}=\sqrt{13}$\text{BC}^2&=3^2+1^2-2\Cdota3\Cdota1\cos120\Deg \\[4pt]
&=10+3=13
\end{align*}

$\text{BD}:\text{DC}=3:1$ であるから
\begin{align*}
&\text{BD}=\dfrac{3}{4}\text{BC}=\dfrac{3\sqrt{13}}{4} \\[4pt]
&\text{CD}=\dfrac{1}{4}\text{BC}=\dfrac{\sqrt{13}}{4}
\end{align*}
&\text{BD}=\dfrac{3}{4}\text{BC}=\dfrac{3\sqrt{13}}{4} \\[4pt]
&\text{CD}=\dfrac{1}{4}\text{BC}=\dfrac{\sqrt{13}}{4}
\end{align*}

性質3より
\begin{align*}
\text{AD}&=\sqrt{3\Cdota1-\dfrac{3\sqrt{13}}{4}\Cdota\dfrac{\sqrt{13}}{4}} \\[4pt]
&=\dfrac{\sqrt{3(16-13)}}{4}=\dfrac{3}{4}
\end{align*}
\text{AD}&=\sqrt{3\Cdota1-\dfrac{3\sqrt{13}}{4}\Cdota\dfrac{\sqrt{13}}{4}} \\[4pt]
&=\dfrac{\sqrt{3(16-13)}}{4}=\dfrac{3}{4}
\end{align*}