放物線と直線で囲まれる部分を直線で二等分する問題について解説します。
最近の入試問題では,出題頻度はかなり少ない問題ですが,出題されても対応できるようにしておきましょう。
また,放物線と直線で囲まれる部分が関連する問題では,6分の1公式を利用できる場合が多いので工夫して計算量を減らすようにしましょう。
2019年 明治大
2019年 明治大放物線 $y=x^2$ と直線 $y=2x+8$ で囲まれた領域を $A$ とする。原点を通る直線 $l$ が領域 $A$ の面積を二等分するとき,直線 $l$ と直線 $y=2x+8$ の交点の $x$ 座標は,$\dfrac{\myhako}{\myhako}$ である。
【解答と考え方】
放物線 $y=x^2$ と直線 $y=2x+8$ の交点を求める。
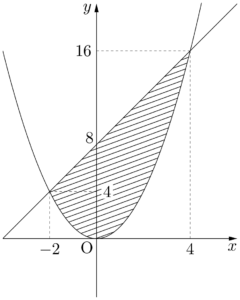
領域 $A$ の面積を $S$ とすると,6分の1公式より
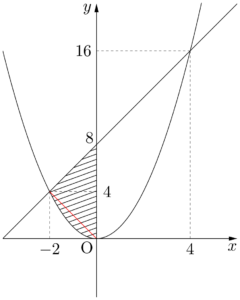
上図の赤線を引いて,領域 $A$ の $y$ 軸より左側の部分の面積を求めると
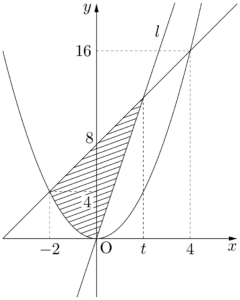
$y$ 軸で2つの部分に分けて $T$ を求めると
放物線 $y=x^2$ と直線 $y=2x+8$ の交点を求める。
\begin{align*}
&x^2-2x-8=0 \\[4pt]
&(x-4)(x+2)=0 \\[4pt]
&x=-2,~4
\end{align*}
領域 $A$ は図の斜線部分である。&x^2-2x-8=0 \\[4pt]
&(x-4)(x+2)=0 \\[4pt]
&x=-2,~4
\end{align*}

領域 $A$ の面積を $S$ とすると,6分の1公式より
\begin{align*}
S=\dfrac{1}{6}\Cdota6^3=36
\end{align*}
S=\dfrac{1}{6}\Cdota6^3=36
\end{align*}

上図の赤線を引いて,領域 $A$ の $y$ 軸より左側の部分の面積を求めると
\begin{align*}
\dfrac{1}{6}\Cdota2^3+\dfrac{1}{2}\Cdota8\Cdota2&=\dfrac{4}{3}+8 \\[4pt]
&=\dfrac{28}{3}<\dfrac{1}{2}S \end{align*}
であるから,$A$ の面積を二等分する直線 $l$ の傾きは正であり,$l$ と直線 $y=2x+8$ の交点の $x$ 座標を $t~(0<t<4)$ とおく。$A$ が $l$ によって分けられる2つの領域のうち,左側の領域の面積を $T$ とすると,$T$ は次の図の斜線部分の面積である。\dfrac{1}{6}\Cdota2^3+\dfrac{1}{2}\Cdota8\Cdota2&=\dfrac{4}{3}+8 \\[4pt]
&=\dfrac{28}{3}<\dfrac{1}{2}S \end{align*}

$y$ 軸で2つの部分に分けて $T$ を求めると
\begin{align*} T&=\dfrac{28}{3}+\dfrac{1}{2}\Cdota8\Cdota t \\[4pt] &=4t+\dfrac{28}{3} \end{align*}
$T=\dfrac{1}{2}S$ であるから \begin{align*} &4t+\dfrac{28}{3}=\dfrac{1}{2}\Cdota36 \\[4pt] &4t=\dfrac{26}{3} \\[4pt] &t=\dfrac{13}{6} \end{align*}
これは $0<t<4$ をみたす。
ヒロ
6分の1公式については,次の記事で説明している。





















