Contents
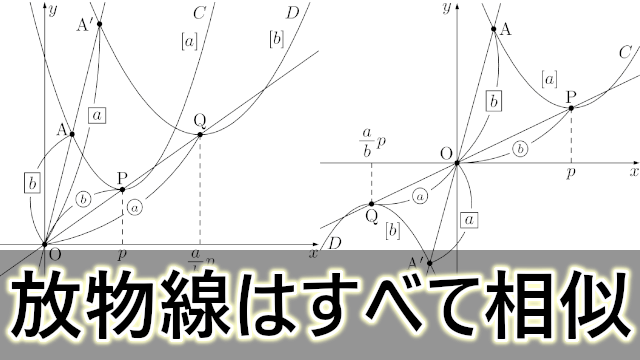
放物線を原点を相似の中心として拡大する

ヒロ
具体的に,放物線 $C:y=\dfrac{1}{2}(x-2)^2+1$ を原点を相似の中心として2倍に拡大してみよう。
下図のように $C$ 上の3点A, B, Cに対して,原点からの距離が2倍になるような点をとると,それぞれP, Q, Rとなる。
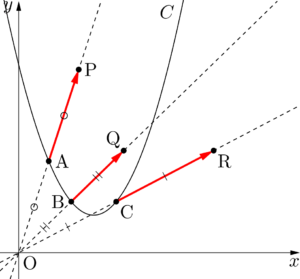


ヒロ
もっとたくさんの点を同じようにとってみよう。
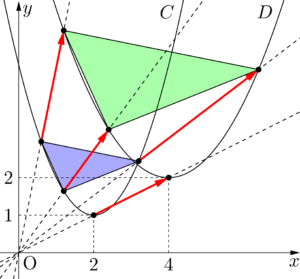
A, B, Cの3点だけでなく,様々な点に対して,同じ操作を行うと次のようになって,なんとなく放物線が見えてくる。



ヒロ
放物線の方程式を具体的に求めてみよう。
$C$ 上の点 $(x,~y)$ の移動先が $(X,~Y)$ であると
\begin{align*}
X=2x,~Y=2y
\end{align*}
が成り立つ。これを変形するとX=2x,~Y=2y
\end{align*}
\begin{align*}
x=\dfrac{X}{2},~y=\dfrac{Y}{2}
\end{align*}
となるから,これを $C:y=\dfrac{1}{2}(x-2)^2+1$ に代入してx=\dfrac{X}{2},~y=\dfrac{Y}{2}
\end{align*}
\begin{align*}
&\dfrac{Y}{2}=\dfrac{1}{2}\left(\dfrac{X}{2}-2\right)^2+1 \\[4pt]
&Y=\dfrac{1}{4}(X-4)^2+2
\end{align*}
&\dfrac{Y}{2}=\dfrac{1}{2}\left(\dfrac{X}{2}-2\right)^2+1 \\[4pt]
&Y=\dfrac{1}{4}(X-4)^2+2
\end{align*}

ヒロ
放物線 $C$ を原点を相似の中心として2倍に拡大すると,放物線 $D:y=\dfrac{1}{4}(x-4)^2+2$ になることが分かったね。
$x^2$ の係数が $\dfrac{1}{2}$ から $\dfrac{1}{4}$ になっていて見た目の形状が異なるため,相似とは思えない。しかし,1つの点,例えば頂点に着目すると,$(2,~1)$ が $(4,~2)$ に移っているから,原点からの距離が2倍になっている。また,対応する3点を結んで三角形を作ると,その2つの三角形はやはり相似の位置にあることが確認できる。


ヒロ
今は具体的に拡大率を2倍にしたが,拡大率と $x^2$ の係数や頂点の座標の間に,どのような関係があるか調べてみよう。