Contents
すべての放物線は相似の位置にあることの証明

ヒロ
それでは,すべての放物線が相似であることを証明しよう。
【証明】
放物線 $C$ のグラフを原点を相似の中心として,$\dfrac{a}{b}~(>0)$ 倍にしたグラフ $D$ も放物線であることを証明する。
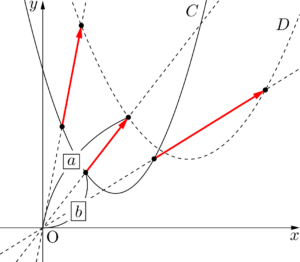
放物線 $C$ 上の点 $\mathrm{A}(x,~y)$ の移動後の点を $\mathrm{A}'(X,~Y)$ とすると,
$\Vec{OA’}=\dfrac{a}{b}\Vec{OA}$ より
したがって,放物線 $C:y=a(x-p)^2+q~(a>0)$ のグラフと放物線 $D:y=b\left(x-\dfrac{a}{b}p\right)^2+\dfrac{a}{b}q$ のグラフは相似の位置にある。このとき,相似の中心は原点であり,相似比は $\abs{b}:\abs{a}$ である。
放物線 $C$ のグラフを原点を相似の中心として,$\dfrac{a}{b}~(>0)$ 倍にしたグラフ $D$ も放物線であることを証明する。

放物線 $C$ 上の点 $\mathrm{A}(x,~y)$ の移動後の点を $\mathrm{A}'(X,~Y)$ とすると,
$\Vec{OA’}=\dfrac{a}{b}\Vec{OA}$ より
\begin{align*}
X=\dfrac{a}{b}x\,,~~Y=\dfrac{a}{b}y
\end{align*}
が成り立つ。これを変形してX=\dfrac{a}{b}x\,,~~Y=\dfrac{a}{b}y
\end{align*}
\begin{align*}
x=\dfrac{b}{a}X\,,~~y=\dfrac{b}{a}Y
\end{align*}
となる。点 $\mathrm{A}(x,~y)$ は放物線 $C$ 上にあるからx=\dfrac{b}{a}X\,,~~y=\dfrac{b}{a}Y
\end{align*}
\begin{align*}
&\dfrac{b}{a}Y=a\left(\dfrac{b}{a}X-p\right)^2+q \\[4pt]
&Y=b\left(X-\dfrac{a}{b}p\right)^2+\dfrac{a}{b}q
\end{align*}
よって,移動後の点 $\mathrm{A}'(X,~Y)$ は放物線 $D:y=b\left(x-\dfrac{a}{b}p\right)^2+\dfrac{a}{b}q$ 上にある。&\dfrac{b}{a}Y=a\left(\dfrac{b}{a}X-p\right)^2+q \\[4pt]
&Y=b\left(X-\dfrac{a}{b}p\right)^2+\dfrac{a}{b}q
\end{align*}
したがって,放物線 $C:y=a(x-p)^2+q~(a>0)$ のグラフと放物線 $D:y=b\left(x-\dfrac{a}{b}p\right)^2+\dfrac{a}{b}q$ のグラフは相似の位置にある。このとき,相似の中心は原点であり,相似比は $\abs{b}:\abs{a}$ である。
まとめ

ヒロ
それでは,すべての放物線が相似であることについてまとめておこう。
$x^2$ の係数が $a$ の放物線 $C$ を点O$’$を相似の中心として $\dfrac{a}{b}$ 倍すると,$x^2$ の係数が $b$ の放物線 $D$ に移る。このとき,$C$ 上の点Rが $D$ 上の点Sに移るとすると,$\dfrac{a}{b}$ の符号によらず,常に
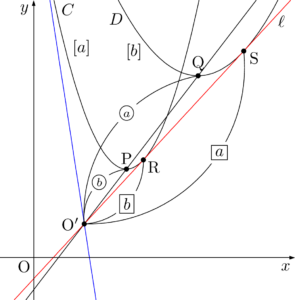
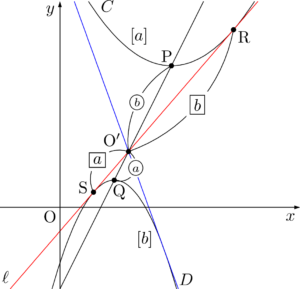
逆に2つの放物線 $C,~D$ が与えられたときは,$x^2$ の係数に着目することによって,簡単に相似の中心O$’$を求めることができる。$a$ と $b$ が同符号のときには,PQを $\abs{b}:\abs{a}$ に外分する点が相似の中心である。$a$ と $b$ が異符号のときには,PQを $\abs{b}:\abs{a}$ に内分する点が相似の中心である。
\begin{align*}
\mathrm{OR}:\mathrm{OS}=\abs{b}:\abs{a}
\end{align*}
が成り立つ。これは2つの放物線 $C,~D$ の頂点をそれぞれP,Qとすると\mathrm{OR}:\mathrm{OS}=\abs{b}:\abs{a}
\end{align*}
\begin{align*}
\mathrm{OP:OQ}=\abs{b}:\abs{a}
\end{align*}
が成り立つということである。ここで,下のグラフにおいて,丸や四角で囲まれた比を表す $a,~b$ はそれぞれ $\abs{a},~\abs{b}$ を表すものとする。\mathrm{OP:OQ}=\abs{b}:\abs{a}
\end{align*}


逆に2つの放物線 $C,~D$ が与えられたときは,$x^2$ の係数に着目することによって,簡単に相似の中心O$’$を求めることができる。$a$ と $b$ が同符号のときには,PQを $\abs{b}:\abs{a}$ に外分する点が相似の中心である。$a$ と $b$ が異符号のときには,PQを $\abs{b}:\abs{a}$ に内分する点が相似の中心である。

ヒロ
すべての放物線が相似であることを利用すると,共通接線も簡単に求めることができる。詳しくは次の記事に書いています。