双曲線は,2つの定点までの距離の差が一定である点の軌跡として定義されます。また,その2つの定点を焦点といいます。
ここでは,双曲線の方程式の導出から始め,焦点の覚え方や媒介変数表示・極方程式など,双曲線の性質を説明します。
Contents
双曲線の方程式の導出

ヒロ
双曲線の方程式を求めよう。
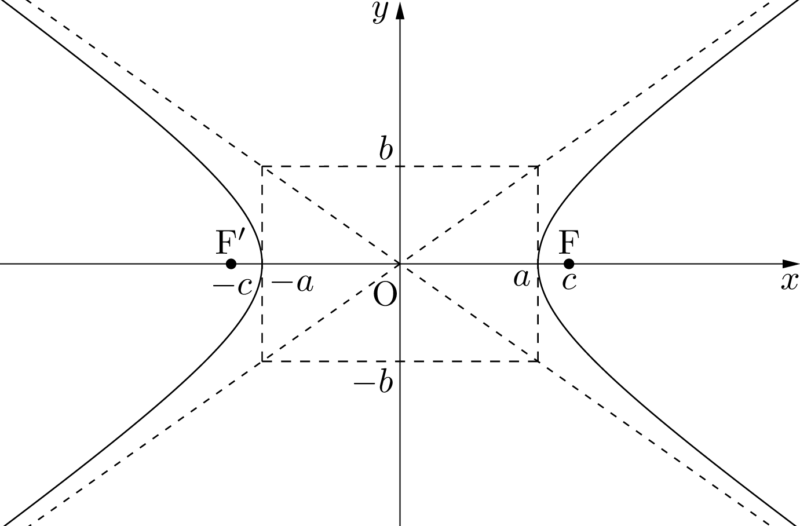
2つの焦点を $\mathrm{F}(c,~0)$, $\mathrm{F}'(-c,~0)$ $(c>0)$ とし,双曲線上の点を $\mathrm{P}(x,~y)$ とする。$\abs{\mathrm{PF}-\mathrm{PF’}}=2a~(c>a>0)$ とすると,
また,焦点の座標を $a,~b$ で表すと
焦点の座標が $\mathrm{F}(0,~c),~\mathrm{F’}(0,-c)$ のとき,方程式は
\begin{align*}
&\abs{\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}}=2a \\[4pt]
&\sqrt{(x-c)^2+y^2}=\pm2a+\sqrt{(x+c)^2+y^2}
\end{align*}
両辺を2乗すると&\abs{\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}}=2a \\[4pt]
&\sqrt{(x-c)^2+y^2}=\pm2a+\sqrt{(x+c)^2+y^2}
\end{align*}
\begin{align*}
&(x-c)^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \\[4pt]
&4cx+4a^2=\pm4a\sqrt{(x+c)^2+y^2} \\[4pt]
&cx+a^2=\pm a\sqrt{(x+c)^2+y^2}
\end{align*}
さらに両辺を2乗すると&(x-c)^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \\[4pt]
&4cx+4a^2=\pm4a\sqrt{(x+c)^2+y^2} \\[4pt]
&cx+a^2=\pm a\sqrt{(x+c)^2+y^2}
\end{align*}
\begin{align*}
&c^2x^2+2ca^2x+a^4=a^2\{(x+c)^2+y^2\} \\[4pt]
&(c^2-a^2)x^2-a^2y^2=a^2c^2-a^4 \\[4pt]
&\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1
\end{align*}
ここで,$c^2-a^2=b^2$ とおくと,双曲線の方程式は&c^2x^2+2ca^2x+a^4=a^2\{(x+c)^2+y^2\} \\[4pt]
&(c^2-a^2)x^2-a^2y^2=a^2c^2-a^4 \\[4pt]
&\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1
\end{align*}
\begin{align*}
&\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1
\end{align*}
となり,グラフは図のようになる。&\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1
\end{align*}

また,焦点の座標を $a,~b$ で表すと
\begin{align*}
\mathrm{F}(\sqrt{a^2+b^2},~0),~~\mathrm{F}'(-\sqrt{a^2+b^2},~0)
\end{align*}
となる。\mathrm{F}(\sqrt{a^2+b^2},~0),~~\mathrm{F}'(-\sqrt{a^2+b^2},~0)
\end{align*}
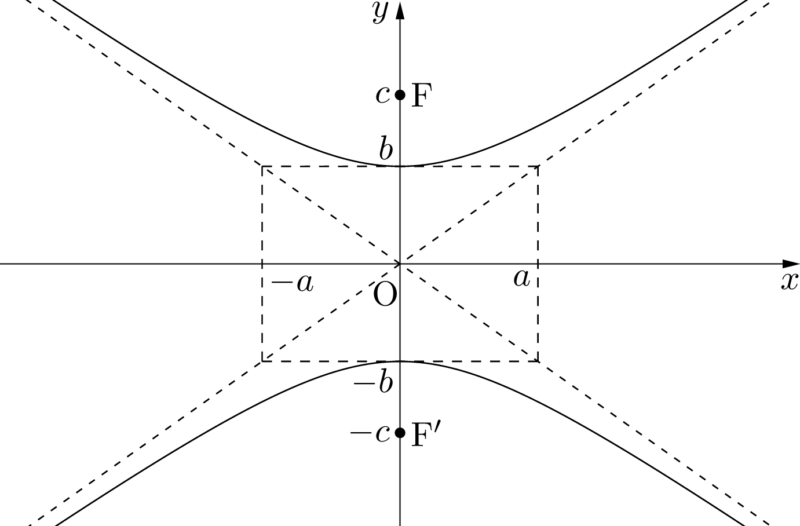
焦点の座標が $\mathrm{F}(0,~c),~\mathrm{F’}(0,-c)$ のとき,方程式は
\begin{align*}
&\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1
\end{align*}
となり,焦点までの距離の差は $2b$ となる。また,グラフは次のようになる。&\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1
\end{align*}



















