Contents
双曲線に関する入試問題【2019年 群馬大】
2019年 群馬大原点を中心とする半径 $\sqrt{3}$ の円 $C_1$ と媒介変数 $\theta$ を用いて $x=\dfrac{1}{\cos\theta}$, $y=\tan\theta$ $\left(-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}\right)$ で表される曲線 $C_2$ について,次の問に答えよ。
(1) $C_1$ と $C_2$ の交点で,第1象限にあるものの座標を求めよ。
(2) (1)で求めた交点における $C_2$ の接線の方程式を求めよ。
(3) $C_1$ と $C_2$ で囲まれた原点を含まない図形を $y$ 軸のまわりに1回転してできる立体の体積を求めよ。
(1) $C_1$ と $C_2$ の交点で,第1象限にあるものの座標を求めよ。
(2) (1)で求めた交点における $C_2$ の接線の方程式を求めよ。
(3) $C_1$ と $C_2$ で囲まれた原点を含まない図形を $y$ 軸のまわりに1回転してできる立体の体積を求めよ。

ヒロ
$C_1$ と $C_2$ の交点を求めるのだから,連立方程式を解こう。
【(1)の解答】
円 $C_1$ の方程式は $x^2+y^2=3$ と表される。$x=\dfrac{1}{\cos\theta}$, $y=\tan\theta$ を代入すると
円 $C_1$ の方程式は $x^2+y^2=3$ と表される。$x=\dfrac{1}{\cos\theta}$, $y=\tan\theta$ を代入すると
\begin{align*}
&\dfrac{1}{\cos^2\theta}+\tan^2\theta=3 \\[4pt]
&(1+\tan^2\theta)+\tan^2\theta=3 \\[4pt]
&\tan^2\theta=1 \\[4pt]
&\tan\theta=\pm1
\end{align*}
求める交点は,第1象限にあるから&\dfrac{1}{\cos^2\theta}+\tan^2\theta=3 \\[4pt]
&(1+\tan^2\theta)+\tan^2\theta=3 \\[4pt]
&\tan^2\theta=1 \\[4pt]
&\tan\theta=\pm1
\end{align*}
\begin{align*}
&\tan\theta=1 \\[4pt]
&\theta=\dfrac{\pi}{4}
\end{align*}
このとき&\tan\theta=1 \\[4pt]
&\theta=\dfrac{\pi}{4}
\end{align*}
\begin{align*}
&x=\dfrac{1}{\cos\dfrac{\pi}{4}}=\sqrt{2} \\[4pt]
&y=\tan\dfrac{\pi}{4}=1
\end{align*}
となるから,求める交点の座標は $(\sqrt{2},~1)$&x=\dfrac{1}{\cos\dfrac{\pi}{4}}=\sqrt{2} \\[4pt]
&y=\tan\dfrac{\pi}{4}=1
\end{align*}

ヒロ
$C_2$ の方程式 $x^2-y^2=1$ を求めて,$C_1$ の方程式と連立することで,$x,~y$ を求めても良い。

ヒロ
(2)は双曲線の接線の方程式の公式を利用しよう。
【(2)の解答】
$C_2$ の方程式は $x^2-y^2=1$ となるから,点$(\sqrt{2},~1)$ における接線の方程式は
$C_2$ の方程式は $x^2-y^2=1$ となるから,点$(\sqrt{2},~1)$ における接線の方程式は
\begin{align*}
&\sqrt{2}x-y=1 \\[4pt]
&y=\sqrt{2}x-1
\end{align*}
&\sqrt{2}x-y=1 \\[4pt]
&y=\sqrt{2}x-1
\end{align*}

ヒロ
(3)は,回転させる図形がどんなものかを把握しよう。
【(3)の解答】
$C_1$ と $C_2$ で囲まれた原点を含まない図形は図の斜線部分である。
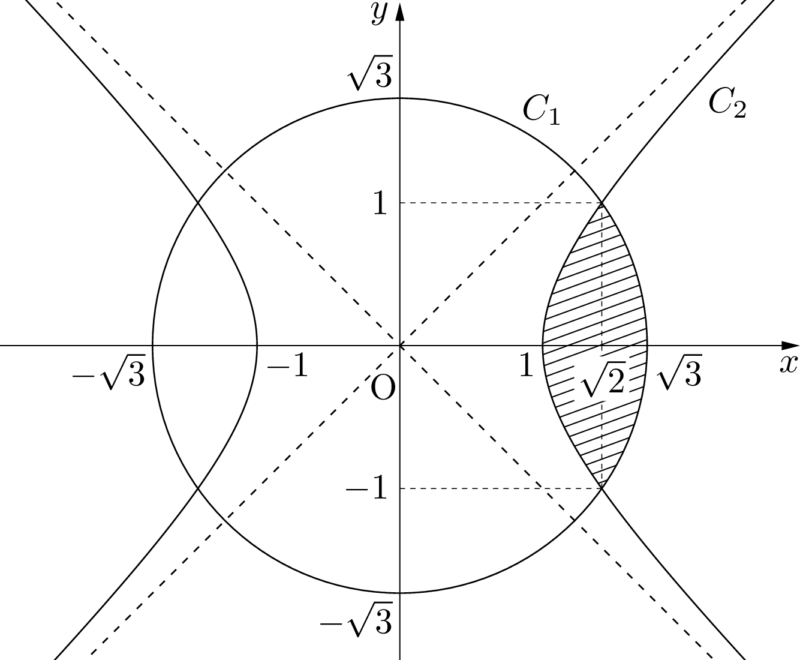
$C_1:x^2+y^2=3$ より,$x^2=3-y^2$
$C_2:x^2-y^2=1$ より,$x^2=y^2+1$
よって,求める体積 $V$ は
$C_1$ と $C_2$ で囲まれた原点を含まない図形は図の斜線部分である。

$C_1:x^2+y^2=3$ より,$x^2=3-y^2$
$C_2:x^2-y^2=1$ より,$x^2=y^2+1$
よって,求める体積 $V$ は
\begin{align*}
V&=\dint{-1}{1}\pi\{(3-y^2)-(y^2+1)\}\;dy \\[4pt]
&=2\pi\dint{0}{1}(-2y^2+2)\;dy \\[4pt]
&=2\pi\Tint{-\dfrac{2}{3}y^3+2y}{0}{1} \\[4pt]
&=2\pi\left(-\dfrac{2}{3}+2\right) \\[4pt]
&=\dfrac{8}{3}\pi
\end{align*}
V&=\dint{-1}{1}\pi\{(3-y^2)-(y^2+1)\}\;dy \\[4pt]
&=2\pi\dint{0}{1}(-2y^2+2)\;dy \\[4pt]
&=2\pi\Tint{-\dfrac{2}{3}y^3+2y}{0}{1} \\[4pt]
&=2\pi\left(-\dfrac{2}{3}+2\right) \\[4pt]
&=\dfrac{8}{3}\pi
\end{align*}
双曲線の性質についてのまとめ

ヒロ
双曲線のグラフ・焦点・極方程式・媒介変数表示・接線の方程式ついて,まとめると次のようになる。
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$
- グラフ
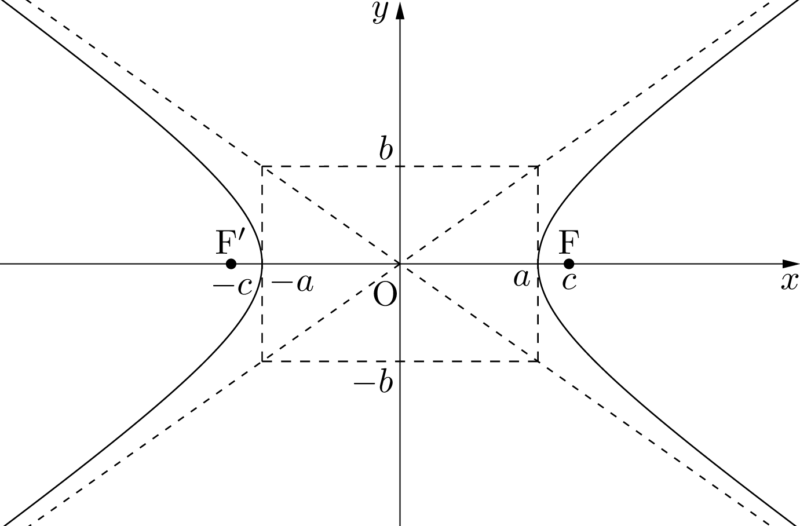
- 焦点の座標\begin{align*}
\mathrm{F}(0,~\sqrt{a^2+b^2}),~\mathrm{F}'(0,~-\sqrt{a^2+b^2})
\end{align*} - 極方程式\begin{align*}ここで $\varepsilon$ と $l$ は
r=\dfrac{l}{1-\varepsilon \cos\theta}
\end{align*}\begin{align*}で定められる定数であり,$\varepsilon$ は離心率と呼ばれる。
\varepsilon=\dfrac{\sqrt{a^2+b^2}}{a},~l=\dfrac{b^2}{a}
\end{align*} - 媒介変数表示\begin{align*}
x=\dfrac{a}{\cos\theta},~~y=b\tan\theta
\end{align*} - 媒介変数表示 その2\begin{align*}
x=\dfrac{a}{2}\left(t+\dfrac{1}{t}\right),~~y=\dfrac{b}{2}\left(t-\dfrac{1}{t}\right)
\end{align*} - 接線の方程式\begin{align*}
\dfrac{x_1x}{a^2}-\dfrac{y_1y}{b^2}=1
\end{align*}
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1$
- グラフ
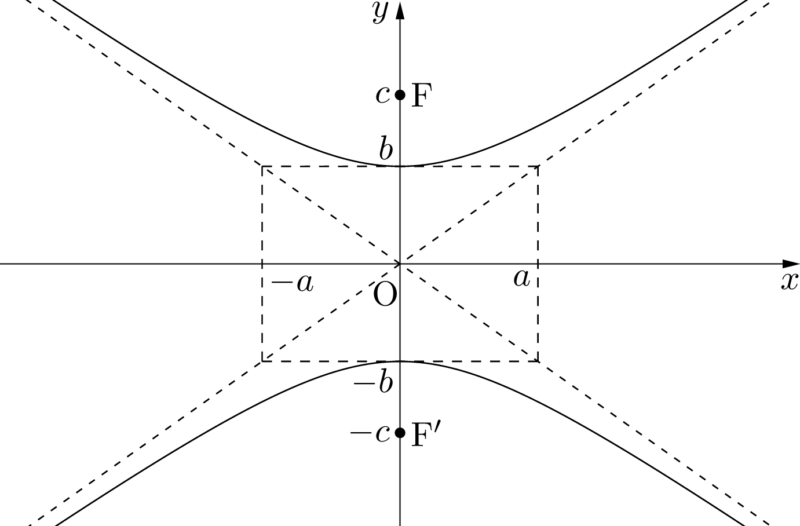
- 焦点の座標\begin{align*}
\mathrm{F}(0,~\sqrt{a^2+b^2}),~\mathrm{F}'(0,~-\sqrt{a^2+b^2})
\end{align*} - 極方程式\begin{align*}ここで $\varepsilon$ と $l$ は
r=\dfrac{l}{1-\varepsilon \cos\theta}
\end{align*}\begin{align*}で定められる定数であり,$\varepsilon$ は離心率と呼ばれる。
\varepsilon=\dfrac{\sqrt{a^2+b^2}}{a},~l=\dfrac{a^2}{b}
\end{align*} - 媒介変数表示\begin{align*}
x=a\tan\theta,~~y=\dfrac{b}{\cos\theta}
\end{align*} - 媒介変数表示 その2\begin{align*}
x=\dfrac{a}{2}\left(t-\dfrac{1}{t}\right),~~y=\dfrac{b}{2}\left(t+\dfrac{1}{t}\right)
\end{align*} - 接線の方程式\begin{align*}
\dfrac{x_1x}{a^2}-\dfrac{y_1y}{b^2}=-1
\end{align*}


















