Contents
双曲線の極方程式

ヒロ
双曲線の極方程式を導出しよう。
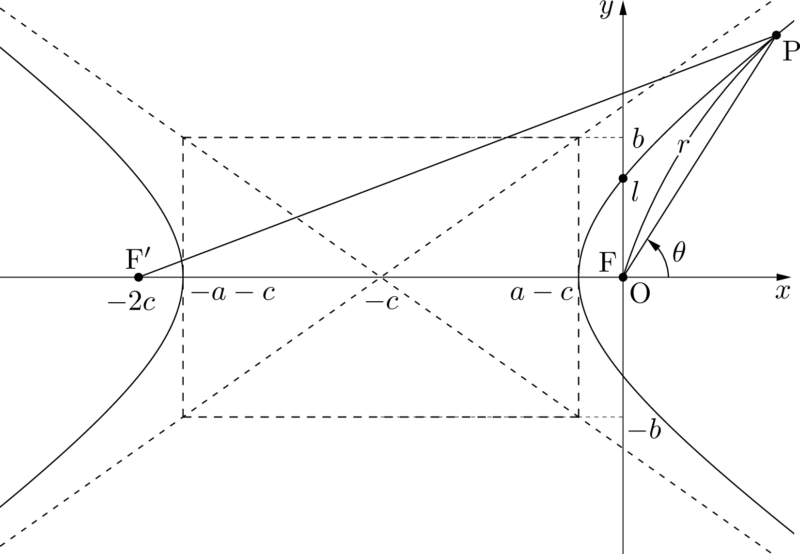
PFと $x$ 軸の正の方向とのなす角を $\theta$ とし,$\mathrm{PF}=r$ とする。
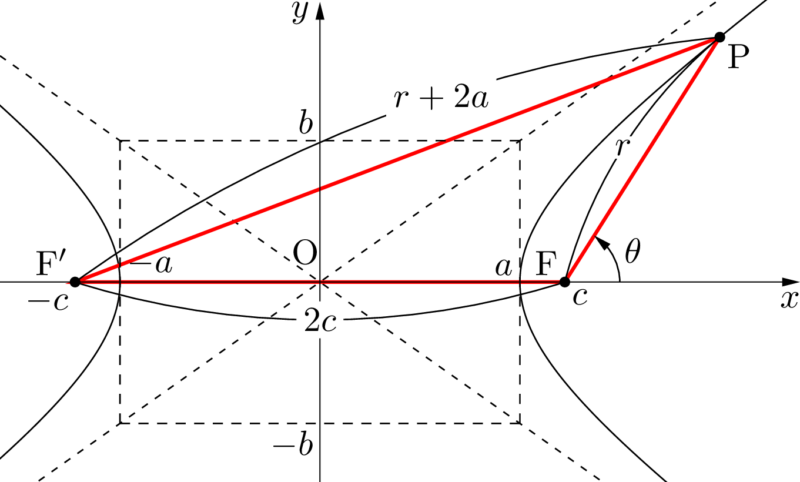
$\mathrm{PF’}-\mathrm{PF}=2a$ より $\mathrm{PF’}=r+2a$ であるから,$\sankaku{PFF’}$ において余弦定理を適用すると

$\mathrm{PF’}-\mathrm{PF}=2a$ より $\mathrm{PF’}=r+2a$ であるから,$\sankaku{PFF’}$ において余弦定理を適用すると
\begin{align*}
&(r+2a)^2=r^2+(2c)^2-2r\Cdota2c\cos(\pi-\theta) \\[4pt]
&4a^2+4ar=4c^2+4rc\cos\theta \\[4pt]
&a^2+ar=c^2+rc\cos\theta \\[4pt]
&r=\dfrac{c^2-ca^2}{a-c\cos\theta} \\[4pt]
&r=\dfrac{\dfrac{c^2-a^2}{a}}{1-\dfrac{c}{a}\cos\theta}
\end{align*}
ここで&(r+2a)^2=r^2+(2c)^2-2r\Cdota2c\cos(\pi-\theta) \\[4pt]
&4a^2+4ar=4c^2+4rc\cos\theta \\[4pt]
&a^2+ar=c^2+rc\cos\theta \\[4pt]
&r=\dfrac{c^2-ca^2}{a-c\cos\theta} \\[4pt]
&r=\dfrac{\dfrac{c^2-a^2}{a}}{1-\dfrac{c}{a}\cos\theta}
\end{align*}
\begin{align*}
\dfrac{c}{a}=\varepsilon,~~\dfrac{c^2-a^2}{a}=l
\end{align*}
とおくと\dfrac{c}{a}=\varepsilon,~~\dfrac{c^2-a^2}{a}=l
\end{align*}
\begin{align*}
r=\dfrac{l}{1-\varepsilon\cos\theta}
\end{align*}
r=\dfrac{l}{1-\varepsilon\cos\theta}
\end{align*}

ヒロ
$\varepsilon=\dfrac{c}{a}$ を離心率ということも覚えておこう。また,$a<c$ より $\varepsilon>1$ であることも分かる。

ヒロ
次に $l$ がどの部分の長さを表しているかを考えよう。
次の図のように,双曲線上の点で $x$ 座標が $c$ の点Qを考えると,実は $\mathrm{QF}=l$ となる。
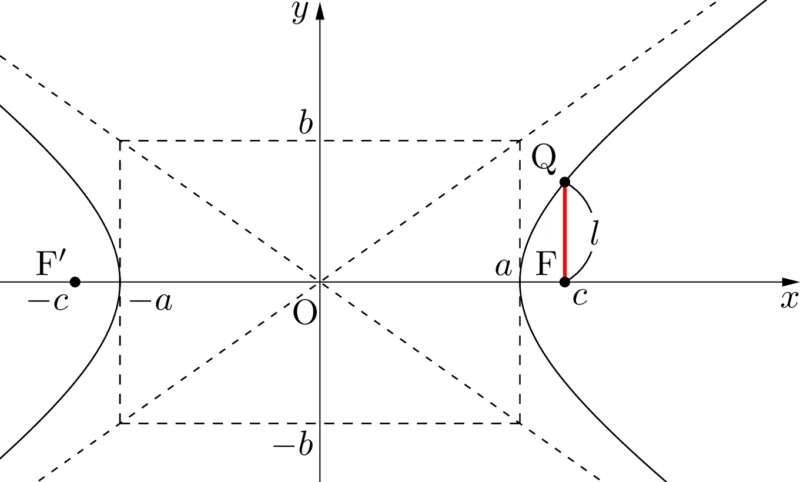
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ を $y~(\geqq0)$ について解くと

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ を $y~(\geqq0)$ について解くと
\begin{align*}
y=\dfrac{b}{a}\sqrt{x^2-a^2}
\end{align*}
となり,$x=c$ を代入すると,y=\dfrac{b}{a}\sqrt{x^2-a^2}
\end{align*}
\begin{align*}
\mathrm{QF}=\dfrac{b}{a}\sqrt{c^2-a^2}
\end{align*}
ここで $b=\sqrt{a^2-c^2}$ であるから\mathrm{QF}=\dfrac{b}{a}\sqrt{c^2-a^2}
\end{align*}
\begin{align*}
\mathrm{QF}=\dfrac{c^2-a^2}{a}~\left(=\dfrac{b^2}{a}\right)
\end{align*}
\mathrm{QF}=\dfrac{c^2-a^2}{a}~\left(=\dfrac{b^2}{a}\right)
\end{align*}

ヒロ
焦点Fからの距離を $r$ としたため,$r=\dfrac{l}{1-\varepsilon\cos\theta}$ のグラフは次の図のようになる。焦点Fが原点の位置にくることに注意しよう。