Contents
双曲線の媒介変数表示

ヒロ
双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 上の点を媒介変数 $\theta$ を用いて表すと,$x=\dfrac{a}{\cos\theta}$, $y=b\tan\theta$ となることを確かめよう。
$x=\dfrac{a}{\cos\theta}$, $y=b\tan\theta$ のとき
\begin{align*}
\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=\dfrac{a^2}{a^2\cos^2\theta}-\dfrac{b^2\tan^2\theta}{b^2} \\[4pt]
&=\dfrac{1}{\cos^2\theta}-\tan^2\theta \\[4pt]
&=1
\end{align*}
となり,点 $\mathrm{P}\left(\dfrac{a}{\cos\theta},~b\tan\theta\right)$ が双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 上にあることが分かる。\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=\dfrac{a^2}{a^2\cos^2\theta}-\dfrac{b^2\tan^2\theta}{b^2} \\[4pt]
&=\dfrac{1}{\cos^2\theta}-\tan^2\theta \\[4pt]
&=1
\end{align*}

ヒロ
$\theta$ と点Pの対応を図で確認してみよう。
原点を中心とする半径 $a$ の円を $C$ とし,$x$ 軸の正の方向となす角が $\theta$ である $C$ 上の点をAとする。直線OAと直線 $x=b$ の交点をB,点Aにおける $C$ の接線と $x$ 軸の交点をCとする。
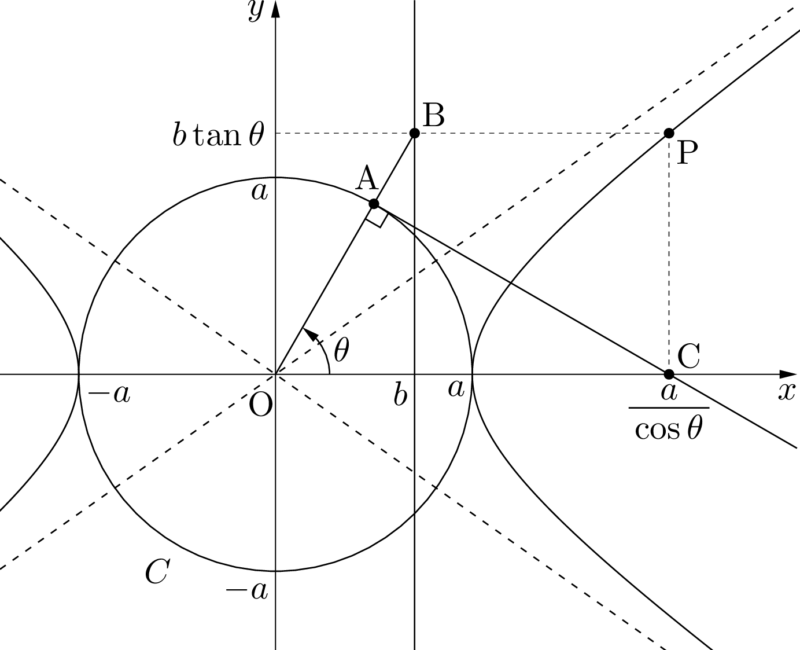
このとき,点Bの $y$ 座標は $b\tan\theta$ である。また,三角形OACに着目することによって,点Cの $x$ 座標が $\dfrac{a}{\cos\theta}$ であることが簡単に分かる。

このとき,点Bの $y$ 座標は $b\tan\theta$ である。また,三角形OACに着目することによって,点Cの $x$ 座標が $\dfrac{a}{\cos\theta}$ であることが簡単に分かる。

ヒロ
このように考えることで,双曲線上の点 $\mathrm{P}\left(\dfrac{a}{\cos\theta},~b\tan\theta\right)$ と $\theta$ の関係が分かる。

ヒロ
ちなみに,双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1$ 上の点を媒介変数 $\theta$ を用いて表すと,$x=a\tan\theta$,$y=\dfrac{b}{\cos\theta}$ となる。
双曲線の媒介変数表示の別の方法

ヒロ
双曲線上の点を媒介変数を用いて表す方法として,次のようなものがあることも知っておこう。
$x=\dfrac{a}{2}\left(t+\dfrac{1}{t}\right)~(t\neq0)$, $y=\dfrac{b}{2}\left(t-\dfrac{1}{t}\right)$ のとき,
\begin{align*}
\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=\dfrac{a^2}{4}\left(t+\dfrac{1}{t}\right)^2-\dfrac{b^2}{4}\left(t-\dfrac{1}{t}\right)^2 \\[4pt]
&=\dfrac{1}{4}\left\{\left(t+\dfrac{1}{t}\right)^2-\left(t-\dfrac{1}{t}\right)^2\right\} \\[4pt]
&=\dfrac{1}{4}\Cdota2t\Cdota\dfrac{2}{t} \\[4pt]
&=1
\end{align*}
よって,点 $\left(\dfrac{a}{2}\left(t+\dfrac{1}{t}\right),~\dfrac{b}{2}\left(t-\dfrac{1}{t}\right)\right)$ は双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 上にある。\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=\dfrac{a^2}{4}\left(t+\dfrac{1}{t}\right)^2-\dfrac{b^2}{4}\left(t-\dfrac{1}{t}\right)^2 \\[4pt]
&=\dfrac{1}{4}\left\{\left(t+\dfrac{1}{t}\right)^2-\left(t-\dfrac{1}{t}\right)^2\right\} \\[4pt]
&=\dfrac{1}{4}\Cdota2t\Cdota\dfrac{2}{t} \\[4pt]
&=1
\end{align*}


















