Contents
双曲線の焦点の覚え方

ヒロ
双曲線の方程式 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=\pm1$ が与えられたときに,焦点の座標がパッと出てこないことがある。また「双曲線の焦点の座標を覚えられない」とか「すぐ忘れる」って言う人は双曲線の定義からサクッと求められるようにしておこう。
双曲線上に点Pをとったとき,2つの焦点F, F$’$ までの距離の差が一定だから,その距離の差を計算しやすい点を考えよう。ここで,焦点Fの $x$ 座標 $c$ は正とする。
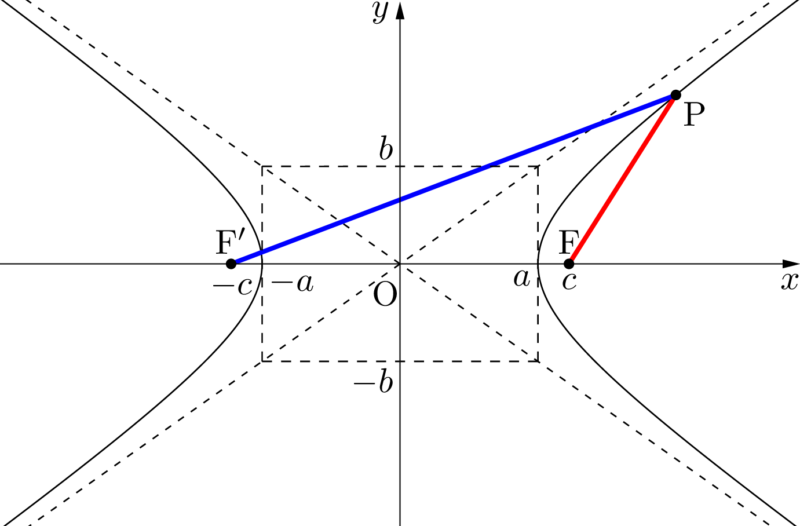
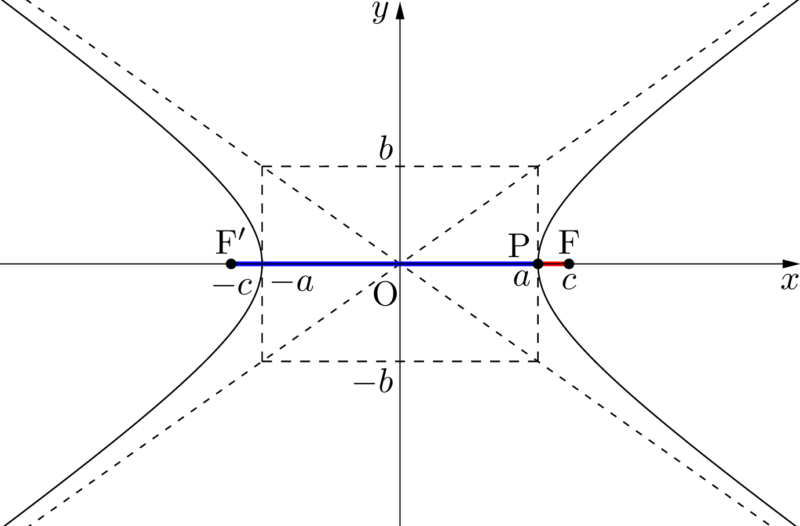
点Pを $(a,~0)$ にとったとき,
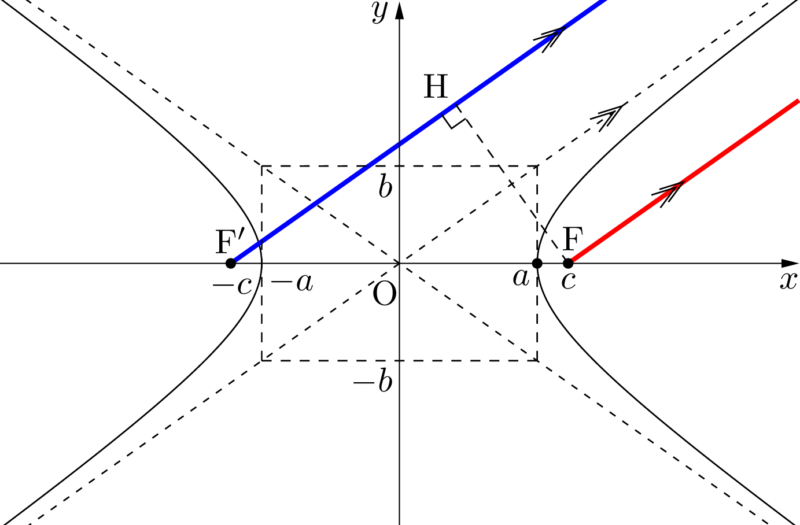
次に点Pを第1象限の無限遠点にとったときを考えると,2直線PFとPF$’$は漸近線と平行になる。

点Pを $(a,~0)$ にとったとき,
\begin{align*}
\mathrm{PF’}-\mathrm{PF}=2a
\end{align*}
であることがすぐに分かる。\mathrm{PF’}-\mathrm{PF}=2a
\end{align*}

次に点Pを第1象限の無限遠点にとったときを考えると,2直線PFとPF$’$は漸近線と平行になる。

点FからPF$’$に下ろした垂線の足をHとすると,$\mathrm{PF’}-\mathrm{PF}=\mathrm{F’H}$ となる。
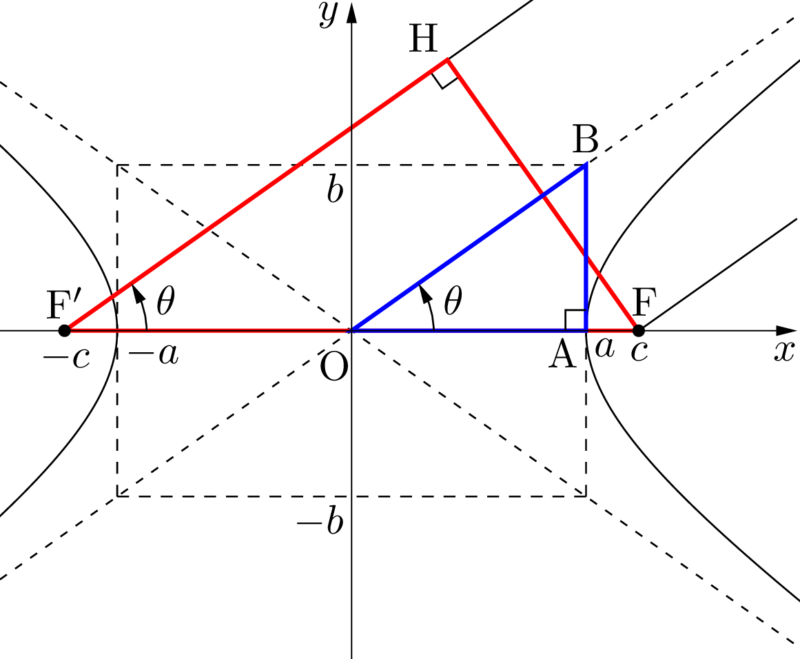
また,三角形OABと三角形F$’$HFは相似な直角三角形であることが分かる。図のように $\theta$ を定めて,三角形OABに着目すると
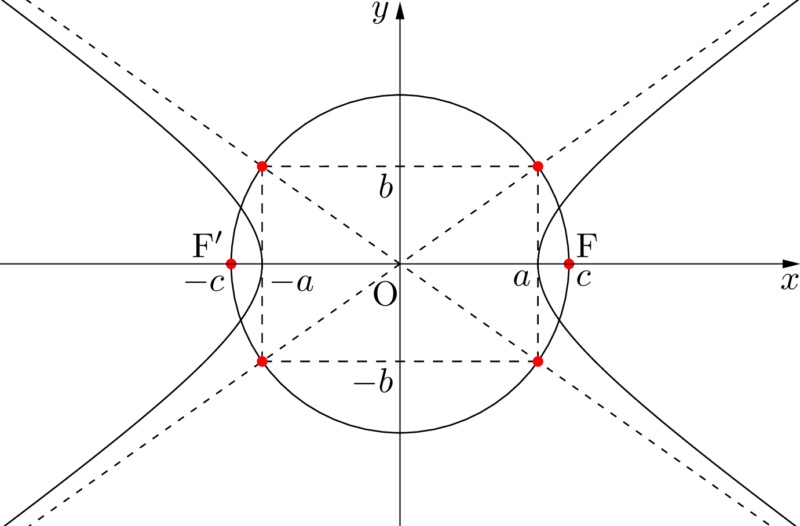
これで焦点Fの座標が $(\sqrt{a^2+b^2},~0)$ であると分かる。また,焦点の座標から,原点を中心とする半径 $\sqrt{a^2+b^2}$ の円を考えると,次のような図が得られる。4つの直線 $x=\pm a,~y=\pm b$ で作られる長方形の外接円は2つの焦点も通ることを覚えておくことで,焦点の座標も簡単に覚えられるかもしれない。

また,三角形OABと三角形F$’$HFは相似な直角三角形であることが分かる。図のように $\theta$ を定めて,三角形OABに着目すると
\begin{align*}
\cos\theta=\dfrac{\mathrm{OA}}{\mathrm{OB}}=\dfrac{a}{\sqrt{a^2+b^2}}
\end{align*}
よって,三角形F$’$HFに着目すると\cos\theta=\dfrac{\mathrm{OA}}{\mathrm{OB}}=\dfrac{a}{\sqrt{a^2+b^2}}
\end{align*}
\begin{align*}
\mathrm{F’H}&=\mathrm{FF’}\cos\theta \\[4pt]
&=2c\cos\theta \\[4pt]
&=\dfrac{2ac}{\sqrt{a^2+b^2}}
\end{align*}
点Pから2焦点までの距離の差は $2a$ であるから,\mathrm{F’H}&=\mathrm{FF’}\cos\theta \\[4pt]
&=2c\cos\theta \\[4pt]
&=\dfrac{2ac}{\sqrt{a^2+b^2}}
\end{align*}
\begin{align*}
&\dfrac{2ac}{\sqrt{a^2+b^2}}=2a \\[4pt]
&c=\sqrt{a^2+b^2}
\end{align*}
&\dfrac{2ac}{\sqrt{a^2+b^2}}=2a \\[4pt]
&c=\sqrt{a^2+b^2}
\end{align*}
これで焦点Fの座標が $(\sqrt{a^2+b^2},~0)$ であると分かる。また,焦点の座標から,原点を中心とする半径 $\sqrt{a^2+b^2}$ の円を考えると,次のような図が得られる。4つの直線 $x=\pm a,~y=\pm b$ で作られる長方形の外接円は2つの焦点も通ることを覚えておくことで,焦点の座標も簡単に覚えられるかもしれない。


ヒロ
忘れないことも重要であるが,忘れたときの対処法を用意しておくことも重要。


















