外積の求め方の記事の最後で,四面体の体積を求める公式について少し触れました。今回は入試問題で出題されている四面体の体積を求めてみましょう。
実際の解答用紙に,外積を利用したことを書くのは気が引けますよね。そこで,外積を利用したときでも,その痕跡を残さず,減点されないような解答の書き方についても説明します。
2018年 山口大・前期

まずはこの問題を解いてみよう!
(1) $\angle\mathrm{BAC}=\theta$ とするとき,$\cos\theta$ の値を求めなさい。
(2) $\triangle\mathrm{ABC}$ の面積 $S$ を求めなさい。
(3) $\triangle\mathrm{ABC}$ を含む平面に垂直なベクトルを $(x,y,1)$ と表すとき,$x,y$ の値をそれぞれ求めなさい。
(4) 原点をOとするとき,四面体OABCの体積 $V$ を求めなさい。

まずは(1)から。ベクトルで $\cos\theta$ といえば内積です!
\begin{cases}
\abs{\Vec{AB}}=\sqrt{2^2+(-1)^2+1^2}=\sqrt{6} \\[4pt]
\abs{\Vec{AC}}=\sqrt{1^2+(-2)^2+5^2}=\sqrt{30} \\[4pt]
\Vec{AB}\Cdot\Vec{AC}=2\Cdot1+(-1)\Cdot(-2)+1\Cdot5=9
\end{cases}
\end{align*}
\cos\theta&=\dfrac{\Vec{AB}\Cdot\Vec{AC}}{\abs{\Vec{AB}}\abs{\Vec{AC}}} \\[4pt]
&=\dfrac{9}{\sqrt{6}\sqrt{30}}=\dfrac{9}{6\sqrt{5}} \\[4pt]
&=\dfrac{3}{2\sqrt{5}}=\dfrac{3\sqrt{5}}{10}
\end{align*}

(2)は $\sin\theta$ を求めて,面積公式を使えば良いはずです。
\sin\theta&=\sqrt{1-\cos^2\theta} \\[4pt]
&=\sqrt{1-\left(\dfrac{3}{2\sqrt{5}}\right)^2} \\[4pt]
&=\sqrt{1-\dfrac{9}{20}}=\dfrac{\sqrt{11}}{2\sqrt{5}}
\end{align*}
S&=\dfrac{1}{2}\abs{\Vec{AB}}\abs{\Vec{AC}}\sin\theta \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{6}\Cdota\sqrt{30}\Cdota\dfrac{\sqrt{11}}{2\sqrt{5}} \\[4pt]
&=\dfrac{3\sqrt{11}}{2}
\end{align*}

(3)は $z$ 成分が1と決められているので,内積が0になることを利用して,連立方程式を解けば良いはずです。
\begin{cases}
2x-y+1=0 \\[4pt]
x-2y+5=0
\end{cases}
\end{align*}

最後は内積の図形的意味を利用すればできるはずです。
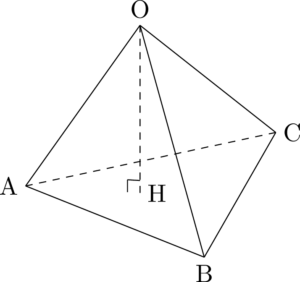
$\vec{n}=(1,3,1)$ より,$\abs{\vec{n}}=\sqrt{11}$ であるから,内積の図形的意味を考えると,
\mathrm{OH}&=\abs{\dfrac{\vec{n}}{\abs{\vec{n}}}\Cdota\Vec{OA}} \\[4pt]
&=\abs{\dfrac{1\Cdot 1+3\Cdot 3+1\Cdot (-2)}{\sqrt{11}}} \\[4pt]
&=\dfrac{8}{\sqrt{11}}
\end{align*}
V&=\dfrac{1}{3}\Cdota S\Cdota\mathrm{OH} \\[4pt]
&=\dfrac{1}{3}\Cdota\dfrac{3\sqrt{11}}{2}\Cdota\dfrac{8}{\sqrt{11}} \\[4pt]
&=4
\end{align*}

出来ました!

じゃあもう1問いってみよう!
2018年 熊本大・前期
(1) $t$ の値を求めよ。
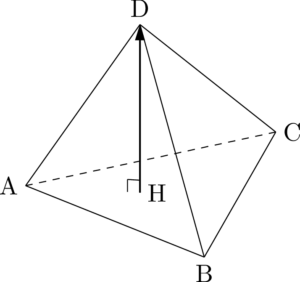
(2) DからA,B,Cを通る平面に垂線を下ろし,A,B,Cを通る平面との交点をHとする。$\Vec{HD}$ を求めよ。
(3) 四面体ABCDの体積を求めよ。

解いていきます!

(1)は「$\angle\mathrm{BAC}$ が直角」とあるから,これをベクトルで表すと $\Vec{AB}\perp\Vec{AC}$ となるので,内積で処理すれば解けるはずですね。
\Vec{AB}=(3,-3,0)=3(1,-1,0),~\Vec{AC}=(t-1,2t-5,t-1)
\end{align*}
&(t-1)-(2t-5)=0 \\
&t=4
\end{align*}

(2)は・・・・
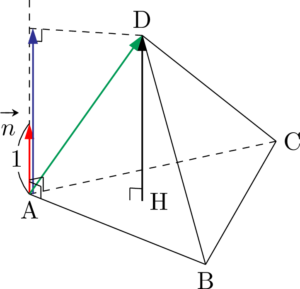
平面ABCに垂直な単位ベクトルを $\vec{n}$ とすると,DHは $\abs{\vec{n}\Cdot\Vec{AD}}$ で表せるけど,外積使って良いのかな・・・
$t=4$ のとき,$\Vec{AC}=(3,3,3)=3(1,1,1)$ となる。
$\vec{b}=(1,-1,0),~\vec{c}=(1,1,1)$ とすると,
&\vec{b}\times\vec{c}=(-1,-1,2) \\[4pt]
&\abs{\vec{b}\times\vec{c}}=\sqrt{(-1)^2+(-1)^2+2^2}=\sqrt{6}
\end{align*}
\mathrm{DH}&=\abs{\dfrac{1}{\sqrt{6}}(\vec{b}\times\vec{c})\Cdota\Vec{AD}} \\[4pt]
&=\abs{\dfrac{0-1+2}{\sqrt{6}}}=\dfrac{1}{\sqrt{6}}
\end{align*}
\Vec{HD}&=\dfrac{1}{\sqrt{6}}\Cdota\dfrac{1}{\sqrt{6}}(-1,-1,2) \\[4pt]
&=\left(-\dfrac{1}{6},-\dfrac{1}{6},\dfrac{1}{3}\right)
\end{align*}

先生,出番です!

はいはい,どうした?

これ解けるんですけど,解答に外積を使ってるのを残すのは微妙ですよね・・・どう書けば良いですか?

なるほど。やってることは合ってるから,外積を表に出さずに,しかも減点されないような書き方を教えてくれということだね。

そうです。

とりあえず外積で $\Vec{AB}$ と $\Vec{AC}$ の両方に垂直なベクトルを出してから,こう書けば良いよ。
&\Vec{AB}\Cdota\vec{n}=\dfrac{1}{\sqrt{6}}(-3+3+0)=0 \\[4pt]
&\Vec{AC}\Cdota\vec{n}=\dfrac{1}{\sqrt{6}}(-3-3+6)=0
\end{align*}
$\Vec{AD}=(0,1,1)$ であるから
\mathrm{DH}&=\abs{\vec{n}\Cdota\Vec{AD}} \\[4pt]
&=\abs{\dfrac{0-1+2}{\sqrt{6}}}=\dfrac{1}{\sqrt{6}}
\end{align*}

このあとは一緒だから省略するよ。

なるほど!とりあえず設定してから内積が0になることを書いて,ちゃんと両方に垂直だと示せば良いんですね!

じゃあ,最後の(3)を解きます。
\Vec{AB}=(3,-3,0),~\Vec{AC}=(3,3,3)
\end{align*}
\abs{\Vec{AB}}=3\sqrt{2},~\abs{\Vec{AC}}=3\sqrt{3}
\end{align*}
\triangle\mathrm{ABC}=\dfrac{1}{2}\Cdota3\sqrt{2}\Cdota3\sqrt{3}=\dfrac{9\sqrt{6}}{2}
\end{align*}
V&=\dfrac{1}{3}\Cdota\triangle\mathrm{ABC}\Cdota\mathrm{DH} \\[4pt]
&=\dfrac{1}{3}\Cdota\dfrac{9\sqrt{6}}{2}\Cdota\dfrac{1}{\sqrt{6}} \\[4pt]
&=\dfrac{3}{2}
\end{align*}

出来ました!

完璧だね。この調子でどんどん解ける問題を増やしていこう!
まとめ

4点の座標が与えられて,四面体の体積を求める問題が出題された場合は,外積を利用して楽に速く求められるようにしよう!

また,外積を利用しても,そのことを解答用紙には残さず減点されない答案を書けるようにするとカンペキだ。