三角関数の基本とも言える加法定理と2倍角の公式と半角の公式の導出について説明します。1999年の東京大学では「三角関数の基本は大丈夫ですか?」と正弦・余弦の定義と加法定理を証明できるかどうかを確認する問題が出題されています。
ということで,三角関数の基本である加法定理を確認しておきましょう。
Contents
1999年 東京大
1999年 東京大(1) 一般角 $\theta$ に対して $\sin\theta,~\cos\theta$ の定義を述べよ。
(2) (1)で述べた定義にもとづき,一般角 $\alpha,~\beta$ に対して
(2) (1)で述べた定義にもとづき,一般角 $\alpha,~\beta$ に対して
\begin{align*}
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\[4pt]
&\cos(\alpha+\beta)=\cos\alpha\sin\beta-\sin\alpha\cos\beta
\end{align*}
を証明せよ。&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\[4pt]
&\cos(\alpha+\beta)=\cos\alpha\sin\beta-\sin\alpha\cos\beta
\end{align*}

ヒロ
まずは,$\sin\theta,~\cos\theta$ の定義をしっかり覚えておこう。
【(1)の解答】
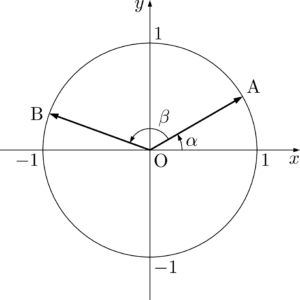
Oを原点とする座標平面において,点 $\mathrm{A}(1,~0)$ をとる。$\Vec{OA}$ を原点のまわりに $\theta$ だけ回転したベクトルを $\Vec{OP}$ とし,点Pの座標を $(x,~y)$ とする。このとき
Oを原点とする座標平面において,点 $\mathrm{A}(1,~0)$ をとる。$\Vec{OA}$ を原点のまわりに $\theta$ だけ回転したベクトルを $\Vec{OP}$ とし,点Pの座標を $(x,~y)$ とする。このとき
\begin{align*}
\sin\theta=y,~\cos\theta=x
\end{align*}
と定義する。\sin\theta=y,~\cos\theta=x
\end{align*}

ヒロ
(2)の加法定理はベクトルを利用して証明しよう。
【(2)の解答】
$\Vec{OA}=(\cos\alpha,~\sin\alpha)$ とし,$\Vec{OA}$ を原点のまわりに $\beta$ だけ回転したベクトルを $\Vec{OB}$ とすると,(1)の定義から
ここで,$\Vec{OA}$ を原点のまわりに $\dfrac{\pi}{2}$ だけ回転したベクトルを $\Vec{OC}$ とすると
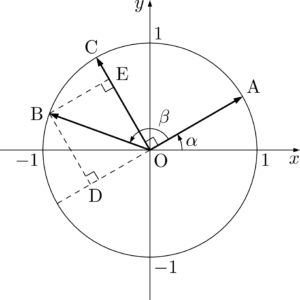
このとき,(1)の定義より
$\Vec{OA}=(\cos\alpha,~\sin\alpha)$ とし,$\Vec{OA}$ を原点のまわりに $\beta$ だけ回転したベクトルを $\Vec{OB}$ とすると,(1)の定義から
\begin{align*}
\Vec{OB}=(\cos(\alpha+\beta),~\sin(\alpha+\beta))~\cdots\cdots①
\end{align*}
となる。\Vec{OB}=(\cos(\alpha+\beta),~\sin(\alpha+\beta))~\cdots\cdots①
\end{align*}

ここで,$\Vec{OA}$ を原点のまわりに $\dfrac{\pi}{2}$ だけ回転したベクトルを $\Vec{OC}$ とすると
\begin{align*}
\Vec{OC}=(-\sin\alpha,~\cos\alpha)
\end{align*}
となり,点Bから直線OC,OAに下ろした垂線の足をそれぞれD,Eとすると次のようになる。\Vec{OC}=(-\sin\alpha,~\cos\alpha)
\end{align*}

このとき,(1)の定義より
\begin{align*}
&\Vec{OD}=\cos\beta\Vec{OA} \\[4pt]
&\Vec{OE}=\sin\beta\Vec{OC}
\end{align*}
となるから&\Vec{OD}=\cos\beta\Vec{OA} \\[4pt]
&\Vec{OE}=\sin\beta\Vec{OC}
\end{align*}
\begin{align*}
\Vec{OB}&=\Vec{OD}+\Vec{OE} \\[4pt]
&=\cos\beta\Vec{OA}+\sin\beta\Vec{OC} \\[4pt]
&=(\cos\alpha\cos\beta,~\sin\alpha\cos\beta)+(-\sin\alpha\sin\beta,~\cos\alpha\sin\beta) \\[4pt]
&=(\cos\alpha\cos\beta-\sin\alpha\sin\beta,~\sin\alpha\cos\beta+\cos\alpha\sin\beta)~\cdots\cdots②
\end{align*}
①,②より\Vec{OB}&=\Vec{OD}+\Vec{OE} \\[4pt]
&=\cos\beta\Vec{OA}+\sin\beta\Vec{OC} \\[4pt]
&=(\cos\alpha\cos\beta,~\sin\alpha\cos\beta)+(-\sin\alpha\sin\beta,~\cos\alpha\sin\beta) \\[4pt]
&=(\cos\alpha\cos\beta-\sin\alpha\sin\beta,~\sin\alpha\cos\beta+\cos\alpha\sin\beta)~\cdots\cdots②
\end{align*}
\begin{align*}
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\[4pt]
&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
\end{align*}
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\[4pt]
&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
\end{align*}


















