Contents
- ページ1
- ページ2
- 1 組立除法と剰余の定理
- ページ3
- 1 累乗の和で表す計算
- ページ4
- 1 組立除法と恒等式
- ページ5
- 1 部分分数分解
- 2 まとめ
累乗の和で表す計算

ヒロ
まずは多項式じゃなくて,整数で考えてみよう。例えば 19 を2の累乗の和で表すとこうなるよね?
\begin{align*}
19=2^4+2^1+2^0
\end{align*}
19=2^4+2^1+2^0
\end{align*}

ヒロ
右から 1の位,2の位,$2^2$ の位・・・として,0, 1 の2種類の数字だけで表すとこうなる。
\begin{align*}
19=2^4+2^1+2^0=10011_{(2)}
\end{align*}
19=2^4+2^1+2^0=10011_{(2)}
\end{align*}

これって2進数ですよね?

ヒロ
そうだね。10進数を2進数に変えるときにはどうやってる?

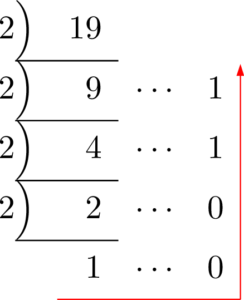
2でどんどん割って,余りを順序を逆に書けば完成です!

ヒロ
そうだね!じゃあ,この割り算がどういう意味をもつかを考えてみよう。
まずは,それぞれの割り算の商と余りを書くと次のようになる。
\begin{align*}
\begin{cases}
19=2\cdot{\color{red}9}+{\color[named]{Cyan}1} \\[4pt]
{\color{red}9}=2\cdot{\color[named]{Green}4}+{\color[named]{YellowOrange}1} \\[4pt]
{\color[named]{Green}4}=2\cdot{\color[named]{Lavender}2}
+{\color[named]{Brown}0} \\[4pt]
{\color[named]{Lavender}2}=2\cdot{\color{blue}1}+{\color[named]{LimeGreen}0}
\end{cases}
\end{align*}
色に注意して,次々と代入すると次のようになる。\begin{cases}
19=2\cdot{\color{red}9}+{\color[named]{Cyan}1} \\[4pt]
{\color{red}9}=2\cdot{\color[named]{Green}4}+{\color[named]{YellowOrange}1} \\[4pt]
{\color[named]{Green}4}=2\cdot{\color[named]{Lavender}2}
+{\color[named]{Brown}0} \\[4pt]
{\color[named]{Lavender}2}=2\cdot{\color{blue}1}+{\color[named]{LimeGreen}0}
\end{cases}
\end{align*}
\begin{align*}
19&=2\cdot{\color{red}9}+{\color[named]{Cyan}1} \\[4pt]
&=2\cdot(2\cdot{\color[named]{Green}4}
+{\color[named]{YellowOrange}1})+{\color[named]{Cyan}1} \\[4pt]
&=2\cdot\{2\cdot(2\cdot{\color[named]{Lavender}2}
+{\color[named]{Brown}0})+{\color[named]{YellowOrange}1}\}+{\color[named]{Cyan}1} \\[4pt]
&=2\cdot\{2\cdot\bigl(2\cdot
(2\cdot{\color{blue}1}+{\color[named]{LimeGreen}0})
+{\color[named]{Brown}0}\bigr)
+{\color[named]{YellowOrange}1}\}+{\color[named]{Cyan}1} \\[4pt]
&={\color{blue}1}\cdot2^4
+{\color[named]{LimeGreen}0}\cdot2^3
+{\color[named]{Brown}0}\cdot2^2
+{\color[named]{YellowOrange}1}\cdot2
+{\color[named]{Cyan}1} \\[4pt]
&={\color{blue}1}{\color[named]{LimeGreen}0}{\color[named]{Brown}0}
{\color[named]{YellowOrange}1}{\color[named]{Cyan}1}_{(2)}
\end{align*}
※入れ子構造の展開の仕組みを理解しよう!19&=2\cdot{\color{red}9}+{\color[named]{Cyan}1} \\[4pt]
&=2\cdot(2\cdot{\color[named]{Green}4}
+{\color[named]{YellowOrange}1})+{\color[named]{Cyan}1} \\[4pt]
&=2\cdot\{2\cdot(2\cdot{\color[named]{Lavender}2}
+{\color[named]{Brown}0})+{\color[named]{YellowOrange}1}\}+{\color[named]{Cyan}1} \\[4pt]
&=2\cdot\{2\cdot\bigl(2\cdot
(2\cdot{\color{blue}1}+{\color[named]{LimeGreen}0})
+{\color[named]{Brown}0}\bigr)
+{\color[named]{YellowOrange}1}\}+{\color[named]{Cyan}1} \\[4pt]
&={\color{blue}1}\cdot2^4
+{\color[named]{LimeGreen}0}\cdot2^3
+{\color[named]{Brown}0}\cdot2^2
+{\color[named]{YellowOrange}1}\cdot2
+{\color[named]{Cyan}1} \\[4pt]
&={\color{blue}1}{\color[named]{LimeGreen}0}{\color[named]{Brown}0}
{\color[named]{YellowOrange}1}{\color[named]{Cyan}1}_{(2)}
\end{align*}

なるほど!こういう意味だったんですね!


















