Contents
- ページ1
- ページ2
- 1 組立除法と剰余の定理
- ページ3
- 1 累乗の和で表す計算
- ページ4
- 1 組立除法と恒等式
- ページ5
- 1 部分分数分解
- 2 まとめ
組立除法と恒等式

ヒロ
今回の問題では,同じようなことを多項式でやれば良いってことになるね。

じゃあ,とりあえず $f(x)$ を $x-1$ でどんどん割っていきますね!
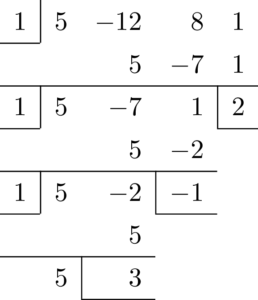

これをさっきと同じように商と余りが分かるように式で書いていきます!

ヒロ
いいね!説明しなくて良いのは楽だわ。
\begin{align*}
\begin{cases}
f(x)=(x-1)(5x^2-7x+1)+2 \\[4pt]
5x^2-7x+1=(x-1)(5x-2)-1 \\[4pt]
5x-2=(x-1)\cdot5+3
\end{cases}
\end{align*}
となるから,順に代入していくと,\begin{cases}
f(x)=(x-1)(5x^2-7x+1)+2 \\[4pt]
5x^2-7x+1=(x-1)(5x-2)-1 \\[4pt]
5x-2=(x-1)\cdot5+3
\end{cases}
\end{align*}
\begin{align*}
f(x)&=(x-1)(5x^2-7x+1)+2 \\[4pt]
&=(x-1)\{(x-1)(5x-2)-1\}+2 \\[4pt]
&=(x-1)\bigl\{(x-1)\bigl((x-1)\cdot5+3\bigr)-1\bigr\}+2 \\[4pt]
&=5(x-1)^3+3(x-1)^2-(x-1)+2
\end{align*}
f(x)&=(x-1)(5x^2-7x+1)+2 \\[4pt]
&=(x-1)\{(x-1)(5x-2)-1\}+2 \\[4pt]
&=(x-1)\bigl\{(x-1)\bigl((x-1)\cdot5+3\bigr)-1\bigr\}+2 \\[4pt]
&=5(x-1)^3+3(x-1)^2-(x-1)+2
\end{align*}

最後に両辺を $(x-1)^4$ で割って完成です。
\begin{align*}
\frac{f(x)}{(x-1)^4}=\frac{5}{x-1}+\frac{3}{(x-1)^2}-\frac{1}{(x-1)^3}+\frac{2}{(x-1)^4}
\end{align*}
\frac{f(x)}{(x-1)^4}=\frac{5}{x-1}+\frac{3}{(x-1)^2}-\frac{1}{(x-1)^3}+\frac{2}{(x-1)^4}
\end{align*}

ヒロ
あとは空欄を見て,$(エ)=3, (オ)=5$ となるね。


















