Contents
- ページ1
- ページ2
- 1 組立除法と剰余の定理
- ページ3
- 1 累乗の和で表す計算
- ページ4
- 1 組立除法と恒等式
- ページ5
- 1 部分分数分解
- 2 まとめ
組立除法と剰余の定理

最初の(ア)と(イ)は組立除法で実際に割り算をすれば求まりますね!

ヒロ
そうだね!
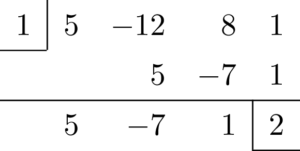
割り算の結果より,
\begin{align*}
(ア)=5x^2-7x+1,\ (イ)=2
\end{align*}
(ア)=5x^2-7x+1,\ (イ)=2
\end{align*}

ヒロ
次の(ウ)はどうする?

次は余りだけを求めれば良いから剰余の定理を使えば良いんですか?
剰余の定理多項式 $f(x)$ を $x-a$ で割ったときの余りは $f(a)$ である。
$g(x)=5x^2-7x+1$ を $x-1$ で割ったときの余りは $g(1)$ だから,
\begin{align*}
&g(1)=5-7+1=-1 \\[4pt]
&(ウ)=-1
\end{align*}
&g(1)=5-7+1=-1 \\[4pt]
&(ウ)=-1
\end{align*}

ヒロ
(ウ)は求まったけど,(エ)と(オ)はどうするの?

それはこれから考えます。

ヒロ
1つずつ解いていくことは重要だけど,入試問題では最初の問題が次の問題の誘導になっていることもあるから,繋がりを考えた方がいいかもね。

ということは割り算と恒等式の関係を考えるってことですか?

ヒロ
元々恒等式の問題なのに,出題者は割り算に着目させているんだ。つまり,今回の恒等式の問題は割り算を使うことで解けますよっていうヒントを与えているんだ。こういうヒントを見逃さないようにしよう。

じゃあ,余りだけじゃなくて商も求めた方が良いってことですか?

ヒロ
そういうことになるね。

さっきの組立除法の下に書いて,もう1回 $x-1$ で割りますね。
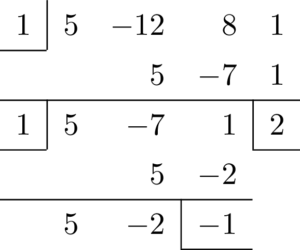

商が $5x-2$ で余りが $-1$ になりました。でも恒等式との関係はよく分かりません。

ヒロ
$(エ)=a, (オ)=b$ として,与えられた恒等式の分母を払ってみようか。
\begin{align*}
f(x)=2-(x-1)+a(x-1)^2+b(x-1)^3
\end{align*}
f(x)=2-(x-1)+a(x-1)^2+b(x-1)^3
\end{align*}

ヒロ
結局 $f(x)$ を $x-1$ の累乗の和で表したいんだね。

これなら前にやったように文字を置き換えれば楽じゃないですか?

ヒロ
確かにそれでも解けるけど,今日は割り算と恒等式の関係を理解して欲しいんだ・・・


















