Contents
180°-θ の三角比

ヒロ
次に $180\Deg-\theta$ の三角比を考えよう。
【$180\Deg-\theta$ の三角比】
原点を中心とする単位円周上の点をPとし,OPと $x$ 軸の正の方向とのなす角 $\kaku{AOP}$ を $180\Deg-\theta$ とする。
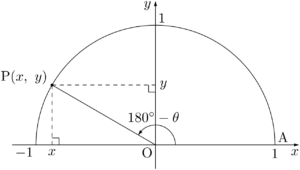
三角比の定義より
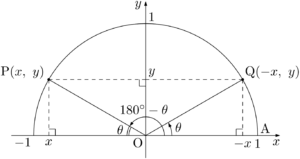
$\kaku{AOQ}=\theta$ であるから
原点を中心とする単位円周上の点をPとし,OPと $x$ 軸の正の方向とのなす角 $\kaku{AOP}$ を $180\Deg-\theta$ とする。

三角比の定義より
\begin{align*}
&\sin(180\Deg-\theta)=y \\[4pt]
&\cos(180\Deg-\theta)=x \\[4pt]
&\tan(180\Deg-\theta)=\dfrac{y}{x}
\end{align*}
となる。ここで $y$ 軸に関して点Pと対称な点をQとすると $\text{Q}(-x,~y)$ となる。&\sin(180\Deg-\theta)=y \\[4pt]
&\cos(180\Deg-\theta)=x \\[4pt]
&\tan(180\Deg-\theta)=\dfrac{y}{x}
\end{align*}

$\kaku{AOQ}=\theta$ であるから
\begin{align*}
&\cos\theta=-x \\[4pt]
&\sin\theta=y \\[4pt]
&\tan\theta=-\dfrac{y}{x}
\end{align*}
したがって&\cos\theta=-x \\[4pt]
&\sin\theta=y \\[4pt]
&\tan\theta=-\dfrac{y}{x}
\end{align*}
\begin{align*}
&\sin(180\Deg-\theta)=\sin\theta \\[4pt]
&\cos(180\Deg-\theta)=-\cos\theta \\[4pt]
&\tan(180\Deg-\theta)=-\tan\theta
\end{align*}
&\sin(180\Deg-\theta)=\sin\theta \\[4pt]
&\cos(180\Deg-\theta)=-\cos\theta \\[4pt]
&\tan(180\Deg-\theta)=-\tan\theta
\end{align*}
90°+θ の三角比

ヒロ
$90\Deg+\theta$ の三角比を考えよう。
【$90\Deg+\theta$ の三角比】
点Aの座標を $(1,~0)$ とする。原点を中心とする単位円周上の点をPとし,OPと $x$ 軸の正の方向とのなす角 $\kaku{AOP}$ を $90\Deg+\theta$ とする。
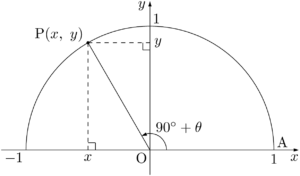
三角比の定義より
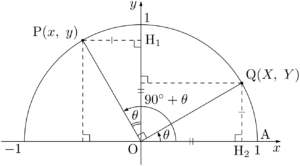
このとき $\sankaku{OPH_1}\equiv\sankaku{OQH_2}$ であるから,符号に注意すると
点Aの座標を $(1,~0)$ とする。原点を中心とする単位円周上の点をPとし,OPと $x$ 軸の正の方向とのなす角 $\kaku{AOP}$ を $90\Deg+\theta$ とする。

三角比の定義より
\begin{align*}
&\sin(90\Deg+\theta)=y \\[4pt]
&\cos(90\Deg+\theta)=x \\[4pt]
&\tan(90\Deg+\theta)=\dfrac{y}{x}
\end{align*}
となる。ここで $\kaku{AOQ}=\theta$ となる点を $\text{Q}(X,~Y)$ とし,点Pから $y$ 軸に下ろした垂線の足をH$_1$,点Qから $x$ 軸に下ろした垂線の足をH$_2$ とする。&\sin(90\Deg+\theta)=y \\[4pt]
&\cos(90\Deg+\theta)=x \\[4pt]
&\tan(90\Deg+\theta)=\dfrac{y}{x}
\end{align*}

このとき $\sankaku{OPH_1}\equiv\sankaku{OQH_2}$ であるから,符号に注意すると
\begin{align*}
X=y,~Y=-x
\end{align*}
となる。よってX=y,~Y=-x
\end{align*}
\begin{align*}
&\sin\theta=Y=-x \\[4pt]
&\cos\theta=X=y \\[4pt]
&\tan\theta=\dfrac{Y}{X}=-\dfrac{x}{y}
\end{align*}
となる。したがって&\sin\theta=Y=-x \\[4pt]
&\cos\theta=X=y \\[4pt]
&\tan\theta=\dfrac{Y}{X}=-\dfrac{x}{y}
\end{align*}
\begin{align*}
&\sin(90\Deg+\theta)=\cos\theta \\[4pt]
&\cos(90\Deg+\theta)=-\sin\theta \\[4pt]
&\tan(90\Deg+\theta)=-\dfrac{1}{\tan\theta}
\end{align*}
&\sin(90\Deg+\theta)=\cos\theta \\[4pt]
&\cos(90\Deg+\theta)=-\sin\theta \\[4pt]
&\tan(90\Deg+\theta)=-\dfrac{1}{\tan\theta}
\end{align*}