Contents
グラグラするとかしないとか

ヒロ
「グラグラするとかしないとか」と呼ばれる簡易法を説明する。

ヒロ
慣れれば3秒で変形できるようになるだろう。
【グラグラするとかしないとか】
まずは次のルールを覚えよう。
「変わる」と「変わらない」は角材の安定度で判断すると覚えやすい。角材が垂直に立っているとき(90°系)はグラグラして不安定だから「変わる」,水平になっているとき(180°系)は安定して「変わらない」という具合に関連付けると忘れないだろう。
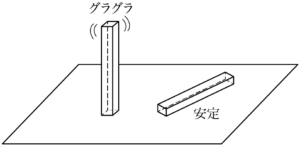
まずは次のルールを覚えよう。
- 90°系は「変わる」,180°系は「変わらない」
- $\theta$ は小さな正の角
- 符号は元の三角比で考える
ここで「変わる」とは
\begin{align*}
&\sin \Longrightarrow \cos \\[4pt]
&\cos \Longrightarrow \sin \\[4pt]
&\tan \Longrightarrow \dfrac{1}{\tan}
\end{align*}
と変わることを表している。逆に「変わらない」は $\sin,~\cos,~\tan$ がそのまま変わらないことを表す。&\sin \Longrightarrow \cos \\[4pt]
&\cos \Longrightarrow \sin \\[4pt]
&\tan \Longrightarrow \dfrac{1}{\tan}
\end{align*}
「変わる」と「変わらない」は角材の安定度で判断すると覚えやすい。角材が垂直に立っているとき(90°系)はグラグラして不安定だから「変わる」,水平になっているとき(180°系)は安定して「変わらない」という具合に関連付けると忘れないだろう。


ヒロ
それでは具体的に説明していく。
【具体的な説明】
$\cos(90\Deg+\theta)$ の書き換えを考える。
まず $90\Deg$ を見て「90°系」と判断する。したがって,符号を無視すると $\cos(90\Deg+\theta)=\sin\theta$ となる。あとは符号が正ならそのままで,負ならマイナスを付けて完成。
符号を考えるときは $\theta$ は小さな正の角として,元の符号を考える。元の符号というのは,今回は $\cos(90\Deg+\theta)$ の符号ということで,点Pの $x$ 座標の符号を考える。簡単に単位円を描くか思い浮かべよう。
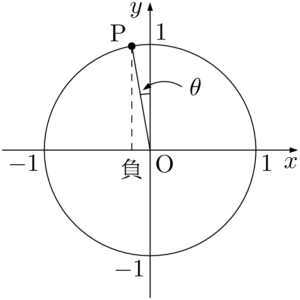
点Pの $x$ 座標は負であるから,マイナスを付けて
$\cos(90\Deg+\theta)$ の書き換えを考える。
まず $90\Deg$ を見て「90°系」と判断する。したがって,符号を無視すると $\cos(90\Deg+\theta)=\sin\theta$ となる。あとは符号が正ならそのままで,負ならマイナスを付けて完成。
符号を考えるときは $\theta$ は小さな正の角として,元の符号を考える。元の符号というのは,今回は $\cos(90\Deg+\theta)$ の符号ということで,点Pの $x$ 座標の符号を考える。簡単に単位円を描くか思い浮かべよう。

点Pの $x$ 座標は負であるから,マイナスを付けて
\begin{align*}
\cos(90\Deg+\theta)=-\sin\theta
\end{align*}
となる。$\sin(90\Deg+\theta)$ の場合は,90°系で「変わる」から $\cos\theta$ で,符号は上図の点Pの $y$ 座標の符号を見て正と分かるから,\cos(90\Deg+\theta)=-\sin\theta
\end{align*}
\begin{align*}
\sin(90\Deg+\theta)=\cos\theta
\end{align*}
となる。$\tan(90\Deg+\theta)$ の場合は「変わる」から $\dfrac{1}{\tan\theta}$ で,符号はOPの傾きを見て負と分かるから\sin(90\Deg+\theta)=\cos\theta
\end{align*}
\begin{align*}
\tan(90\Deg+\theta)=-\dfrac{1}{\tan\theta}
\end{align*}
\tan(90\Deg+\theta)=-\dfrac{1}{\tan\theta}
\end{align*}

ヒロ
次に $180\Deg-\theta$ の三角比を考えよう。
【$180\Deg-\theta$ の三角比】
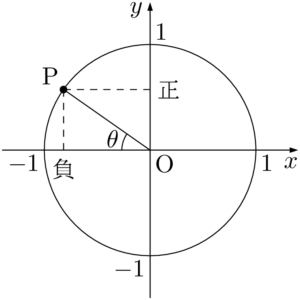
$\cos(180\Deg-\theta)$ の場合,180°系で「変わらない」から $\cos\theta$ で,符号は上図の点Pの $x$ 座標を見て負と分かるから
180°系で「変わらない」からそれぞれ $\sin\theta,~\tan\theta$ で,サインの符号は点Pの $y$ 座標を見て正であり,タンジェントの符号はOPの傾きを見て負であるから

$\cos(180\Deg-\theta)$ の場合,180°系で「変わらない」から $\cos\theta$ で,符号は上図の点Pの $x$ 座標を見て負と分かるから
\begin{align*}
\cos(180\Deg-\theta)=-\cos\theta
\end{align*}
同じようにして $\sin(180\Deg-\theta)$ と $\tan(180\Deg-\theta)$ も考えよう。\cos(180\Deg-\theta)=-\cos\theta
\end{align*}
180°系で「変わらない」からそれぞれ $\sin\theta,~\tan\theta$ で,サインの符号は点Pの $y$ 座標を見て正であり,タンジェントの符号はOPの傾きを見て負であるから
\begin{align*}
&\sin(180\Deg-\theta)=\sin\theta \\[4pt]
&\tan(180\Deg-\theta)=-\tan\theta
\end{align*}
となる。&\sin(180\Deg-\theta)=\sin\theta \\[4pt]
&\tan(180\Deg-\theta)=-\tan\theta
\end{align*}

ヒロ
この方法を身に付けることで,数学Ⅱで角が180°以上に拡張されても柔軟に対応することができる。
【180°以上の角に対応】
例えば $\cos(180\Deg+\theta)$ の場合は,180°系で「変わらない」から,符号を無視して $\cos\theta$ となる。
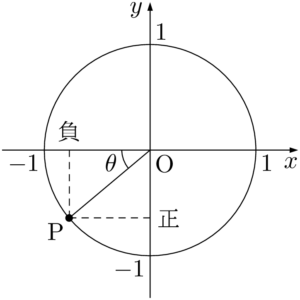
符号は上図の点Pの $x$ 座標を見て負であるから,
例えば $\cos(180\Deg+\theta)$ の場合は,180°系で「変わらない」から,符号を無視して $\cos\theta$ となる。

符号は上図の点Pの $x$ 座標を見て負であるから,
\begin{align*}
\cos(180\Deg+\theta)=-\cos\theta
\end{align*}
となる。サインやタンジェントも同様に考えて\cos(180\Deg+\theta)=-\cos\theta
\end{align*}
\begin{align*}
&\sin(180\Deg+\theta)=-\sin\theta \\[4pt]
&\tan(180\Deg+\theta)=\tan\theta
\end{align*}
となることがすぐに分かるだろう。&\sin(180\Deg+\theta)=-\sin\theta \\[4pt]
&\tan(180\Deg+\theta)=\tan\theta
\end{align*}
90°±θ,180°-θ の三角比のまとめ

ヒロ
$90\Deg\pm\theta,~180\Deg-\theta$ の三角比をまとめておく。
三角比の変形のまとめ
- $\sin(90\Deg-\theta)=\cos\theta$
- $\cos(90\Deg-\theta)=\sin\theta$
- $\tan(90\Deg-\theta)=\dfrac{1}{\tan\theta}$
- $\sin(180\Deg-\theta)=\sin\theta$
- $\cos(180\Deg-\theta)=-\cos\theta$
- $\tan(180\Deg-\theta)=-\tan\theta$
- $\cos(90\Deg+\theta)=-\sin\theta$
- $\sin(90\Deg+\theta)=\cos\theta$
- $\tan(90\Deg+\theta)=-\dfrac{1}{\tan\theta}$