ここでは三角比の変形について解説します。
90°±θや180°-θの三角比が現れたときに変形できるようにしましょう。
定義に基づいた方法と簡易法「グラグラするとかしないとか」について説明します。
Contents
90°-θ の三角比

ヒロ
まずは $90\Deg-\theta$ の三角比を考えよう。
【$90\Deg-\theta$ の三角比】
$\kaku{A}=\theta$ である三角形ABCを考える。このとき $\kaku{C}=90\Deg-\theta$ となり,考えやすいように向きを変えたものを並べると次のようになる。
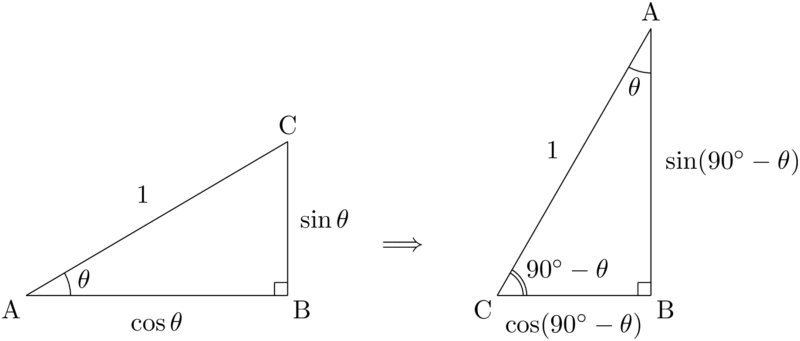
三角形ABCにおいて斜辺ACの長さを1とすると,
$\kaku{A}=\theta$ である三角形ABCを考える。このとき $\kaku{C}=90\Deg-\theta$ となり,考えやすいように向きを変えたものを並べると次のようになる。

三角形ABCにおいて斜辺ACの長さを1とすると,
\begin{align*}
\text{AB}=\cos\theta,~\text{BC}=\sin\theta
\end{align*}
である。三角形ABCの向きを変えて $90\Deg-\theta$ に着目すると,\text{AB}=\cos\theta,~\text{BC}=\sin\theta
\end{align*}
\begin{align*}
\text{AB}=\sin(90\Deg-\theta),~\text{BC}=\cos(90\Deg-\theta)
\end{align*}
と表すことができる。ABとBCの長さを2通りの方法で表したが,元が同じ三角形で向きを変えただけだから,それぞれの辺の長さは等しい。したがって\text{AB}=\sin(90\Deg-\theta),~\text{BC}=\cos(90\Deg-\theta)
\end{align*}
\begin{align*}
&\sin(90\Deg-\theta)=\cos\theta \\[4pt]
&\cos(90\Deg-\theta)=\sin\theta
\end{align*}
また,右側の三角形で $\dfrac{\text{AB}}{\text{BC}}=\dfrac{\sin(90\Deg-\theta)}{\cos(90\Deg-\theta)}$ であり,左側の三角形では $\dfrac{\text{AB}}{\text{BC}}=\dfrac{\cos\theta}{\sin\theta}$ であるから&\sin(90\Deg-\theta)=\cos\theta \\[4pt]
&\cos(90\Deg-\theta)=\sin\theta
\end{align*}
\begin{align*}
&\dfrac{\sin(90\Deg-\theta)}{\cos(90\Deg-\theta)}=\dfrac{\cos\theta}{\sin\theta} \\[4pt]
&\tan(90\Deg-\theta)=\dfrac{1}{\tan\theta}
\end{align*}
&\dfrac{\sin(90\Deg-\theta)}{\cos(90\Deg-\theta)}=\dfrac{\cos\theta}{\sin\theta} \\[4pt]
&\tan(90\Deg-\theta)=\dfrac{1}{\tan\theta}
\end{align*}