ここでは多項式の割り算を利用する問題について説明します。
大学入試問題の中には,問題を一見しただけでは,割り算を利用する問題だと分からない問題もあります。
多項式の割り算には,単に割り算をするだけでない利用法があります。
新たな利用法を習得することによって,計算を楽にできるようにしましょう。
Contents
多項式の割り算を次数下げに利用する

ヒロ
多項式にある値を代入して,その値を求める問題では割り算を利用することで計算が楽になることがある。
【次数を下げて計算を楽にする】
いま,多項式 $f(x)$ に $x=a$ を代入した値 $f(a)$ を求めたいとする。
ここで $a$ が $g(a)=0$ をみたすとすると,$f(x)\div g(x)$ を考えることで計算を楽にすることができる場合がある。$f(x)$ を $g(x)$ で割ったときの商を $Q(x)$,余りを $R(x)$ とすると
$g(x)$ の次数が $f(x)$ の次数より低ければ,$R(x)$ の次数は $f(x)$ の次数より2以上低くなる。したがって,$f(a)$ を計算するより,$R(a)$ を計算した方が楽に計算できることになる。ただし,割り算に時間がかかりすぎると,この工夫は意味をなさないかもしれない。直接 $f(a)$ を計算するか工夫をするかの判断を短時間ですることが重要である。
いま,多項式 $f(x)$ に $x=a$ を代入した値 $f(a)$ を求めたいとする。
ここで $a$ が $g(a)=0$ をみたすとすると,$f(x)\div g(x)$ を考えることで計算を楽にすることができる場合がある。$f(x)$ を $g(x)$ で割ったときの商を $Q(x)$,余りを $R(x)$ とすると
\begin{align*}
f(x)=g(x)Q(x)+R(x)
\end{align*}
が成り立つ。$x=a$ を代入すると,f(x)=g(x)Q(x)+R(x)
\end{align*}
\begin{align*}
&f(a)=g(a)Q(a)+R(a)
\end{align*}
となり,$g(a)=0$ であるから,$f(a)=R(a)$ となる。&f(a)=g(a)Q(a)+R(a)
\end{align*}
$g(x)$ の次数が $f(x)$ の次数より低ければ,$R(x)$ の次数は $f(x)$ の次数より2以上低くなる。したがって,$f(a)$ を計算するより,$R(a)$ を計算した方が楽に計算できることになる。ただし,割り算に時間がかかりすぎると,この工夫は意味をなさないかもしれない。直接 $f(a)$ を計算するか工夫をするかの判断を短時間ですることが重要である。
多項式の割り算を利用する問題
2019年 青山学院大$x=\dfrac{\sqrt{5}-3}{2}$ のとき,$x^2+3x=\myhako$ であり,$2x^4+5x^3-3x^2-x+7=\myhako\sqrt{\myhako}$ である。
【考え方と解答】
$x^2+3x$ を $x=\dfrac{\sqrt{5}-3}{2}$ に代入しても良いが,面白くないので少し工夫をする。
$(2x^4+5x^3-3x^2-x+7)\div(x^2+3x+1)$ を計算すると,次のようになる。
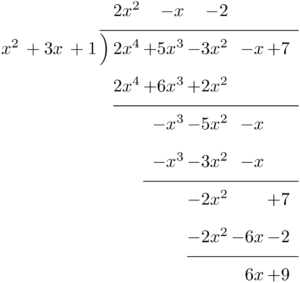
割り算の結果より
$x^2+3x$ を $x=\dfrac{\sqrt{5}-3}{2}$ に代入しても良いが,面白くないので少し工夫をする。
\begin{align*}
x^2+3x&=x(x+3) \\[4pt]
&=\dfrac{\sqrt{5}-3}{2}\Cdota\dfrac{\sqrt{5}+3}{2} \\[4pt]
&=\dfrac{5-9}{4}=-1
\end{align*}
よって $x^2+3x+1=0$ が成り立つから,これを利用して与えられた4次式の値を求めよう。x^2+3x&=x(x+3) \\[4pt]
&=\dfrac{\sqrt{5}-3}{2}\Cdota\dfrac{\sqrt{5}+3}{2} \\[4pt]
&=\dfrac{5-9}{4}=-1
\end{align*}
$(2x^4+5x^3-3x^2-x+7)\div(x^2+3x+1)$ を計算すると,次のようになる。

割り算の結果より
\begin{align*}
2x^4+5x^3-3x^2-x+7=(x^2+3x+1) (2x^2-x-2)+6x+9
\end{align*}
となるから,求める値は2x^4+5x^3-3x^2-x+7=(x^2+3x+1) (2x^2-x-2)+6x+9
\end{align*}
\begin{align*}
6\Cdota\dfrac{\sqrt{5}-3}{2}+9=3\sqrt{5}
\end{align*}
6\Cdota\dfrac{\sqrt{5}-3}{2}+9=3\sqrt{5}
\end{align*}