Contents
多項定理に関する入試問題2
2020年 愛知医科大$(a+b+c+d)^8$ の展開式における $a^3b^3cd$ の係数を求めよ。
【考え方と解答】
8個の括弧において,$a$ を3個,$b$ を3個,$c,~d$ を1個ずつ選ぶときを考えて,求める係数は
8個の括弧において,$a$ を3個,$b$ を3個,$c,~d$ を1個ずつ選ぶときを考えて,求める係数は
\begin{align*}
\dfrac{8!}{3!3!}=\dfrac{8\Cdot7\Cdot6\Cdot5\Cdot4}{3\Cdot2\Cdot1}=1120
\end{align*}
\dfrac{8!}{3!3!}=\dfrac{8\Cdot7\Cdot6\Cdot5\Cdot4}{3\Cdot2\Cdot1}=1120
\end{align*}
多項定理に関する入試問題3
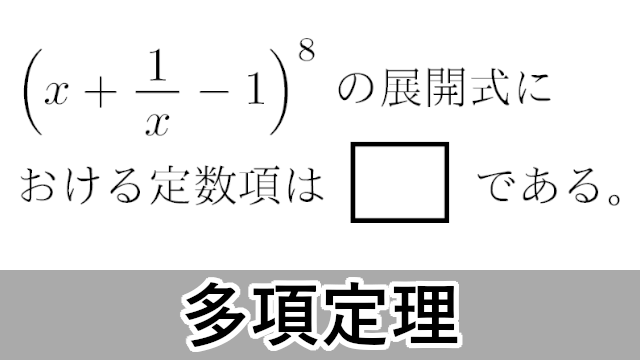
2017年 福岡大・医$\left(x+\dfrac{1}{x}-1\right)^8$ の展開式における定数項は $\myhako$ である。
【考え方と解答】
$\left(x+\dfrac{1}{x}-1\right)^8$ の展開式の一般項は
定数項は $p-q=0$ となるときだから
$\left(x+\dfrac{1}{x}-1\right)^8$ の展開式の一般項は
\begin{align*}
\dfrac{8!}{p!q!r!}x^p\left(\dfrac{1}{x}\right)^q(-1)^r=\dfrac{8!}{p!q!r!}\Cdota(-1)^rx^{p-q}
\end{align*}
と表せる。ただし,$p,~q,~r$ は $p+q+r=8$ をみたす0以上の整数とする。\dfrac{8!}{p!q!r!}x^p\left(\dfrac{1}{x}\right)^q(-1)^r=\dfrac{8!}{p!q!r!}\Cdota(-1)^rx^{p-q}
\end{align*}
定数項は $p-q=0$ となるときだから
\begin{align*}
(p,~q,~r)=(0,~0,~8),~(1,~1,~6),~(2,~2,~4),~(3,~3,~2),~(4,~4,~0)
\end{align*}
の5つの場合がある。よって,求める定数項は(p,~q,~r)=(0,~0,~8),~(1,~1,~6),~(2,~2,~4),~(3,~3,~2),~(4,~4,~0)
\end{align*}
\begin{align*}
&\dfrac{8!}{8!}\Cdota(-1)^8+\dfrac{8!}{6!}\Cdota(-1)^6+\dfrac{8!}{2!2!4!}\Cdota(-1)^4+\dfrac{8!}{3!3!2!}\Cdota(-1)^2+\dfrac{8!}{4!4!} \\[4pt]
&=1+56+420+560+70=1107
\end{align*}
&\dfrac{8!}{8!}\Cdota(-1)^8+\dfrac{8!}{6!}\Cdota(-1)^6+\dfrac{8!}{2!2!4!}\Cdota(-1)^4+\dfrac{8!}{3!3!2!}\Cdota(-1)^2+\dfrac{8!}{4!4!} \\[4pt]
&=1+56+420+560+70=1107
\end{align*}