Contents
多項定理を理解しよう

ヒロ
それでは多項定理の意味を理解しよう。
【多項定理の意味】
$(a+b+c)^n=(a+b+c)(a+b+c)\cdots(a+b+c)$ であるから,当たり前のことであるが,$a+b+c$ が $n$ 個かけられている。$n$ 個のうち,$a$ を $p$ 個,$b$ を $q$ 個,$c$ を $r$ 個選んだときにできる項は $a^pb^qc^r$ である。ただし,$p+q+r=n$ とする。また,選び方を考えると,$p$ 個の $a$,$q$ 個の $b$,$r$ 個の $c$ を一列に並べる方法を考えて
$(a+b+c)^n=(a+b+c)(a+b+c)\cdots(a+b+c)$ であるから,当たり前のことであるが,$a+b+c$ が $n$ 個かけられている。$n$ 個のうち,$a$ を $p$ 個,$b$ を $q$ 個,$c$ を $r$ 個選んだときにできる項は $a^pb^qc^r$ である。ただし,$p+q+r=n$ とする。また,選び方を考えると,$p$ 個の $a$,$q$ 個の $b$,$r$ 個の $c$ を一列に並べる方法を考えて
\begin{align*}
\dfrac{(p+q+r)!}{p!q!r!}=\dfrac{n!}{p!q!r!}
\end{align*}
通りあることが分かるから,一般項は $\dfrac{n!}{p!q!r!}a^pb^qc^r$ となる。\dfrac{(p+q+r)!}{p!q!r!}=\dfrac{n!}{p!q!r!}
\end{align*}
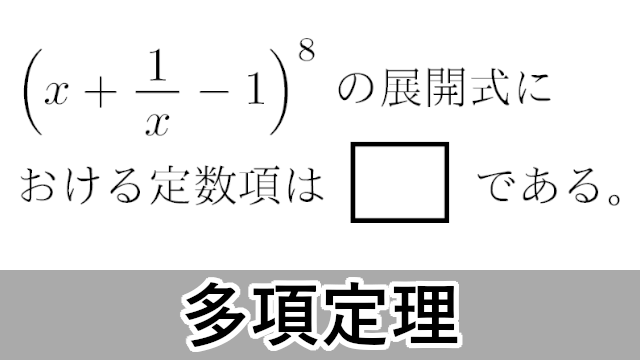
多項定理に関する入試問題
2013年 北里大・医$(x+2y+3z)^6$ の展開式における $x^4y^2$ の係数は $\myhako$ であり,$x^3y^2z$ の係数は $\myhako$ である。
【考え方と解答】
多項定理の考え方を利用しよう。$x^4y^2$ の項になるのは,6個の括弧のうち,$x$ を4個,$2y$ を2個選ぶときだから,$x^4y^2$ の係数は
多項定理の考え方を利用しよう。$x^4y^2$ の項になるのは,6個の括弧のうち,$x$ を4個,$2y$ を2個選ぶときだから,$x^4y^2$ の係数は
\begin{align*}
\dfrac{6!}{4!2!}\Cdota2^2=15\times4=60
\end{align*}
$x^3y^2z$ の項になるのは,6個の括弧のうち,$x$ を3個,$2y$ を2個,$3z$ を1個選ぶときだから,$x^3y^2z$ の係数は\dfrac{6!}{4!2!}\Cdota2^2=15\times4=60
\end{align*}
\begin{align*}
\dfrac{6!}{3!2!}\Cdota2^2\Cdota3=60\times12=720
\end{align*}
\dfrac{6!}{3!2!}\Cdota2^2\Cdota3=60\times12=720
\end{align*}