Contents
放物線の性質【パラボラアンテナ】

ヒロ
放物線を軸のまわりに回転させた曲面は放物面と呼ばれ,有名なものにパラボラアンテナが挙げられる。

ヒロ
パラボラアンテナがアンテナとして機能する理由を知るために,放物線・放物面の性質を知っておこう。
例題放物線 $C$ を $y^2=4px~(p>0)$ とする。$x$ 軸に平行な光線が $C$ 上の点 $\mathrm{A}(a,~b)$ で反射したとき,反射光は必ず焦点Fを通ることを示せ。
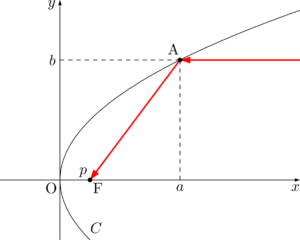

【証明】
点Aにおける $C$ の接線を $l$ とし,点Aを通り $x$ 軸と平行な直線を $m$ とする。2直線 $m$, AF の角の二等分線が $l$ に一致することを証明する。
$y^2=4px$ の両辺を $x$ で微分すると
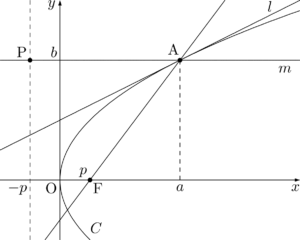
$C$ の準線は $x=-p$ であり,焦点Fの座標は $(p,~0)$ である。また,準線と直線 $m$ の交点をPとすると
点Aにおける $C$ の接線を $l$ とし,点Aを通り $x$ 軸と平行な直線を $m$ とする。2直線 $m$, AF の角の二等分線が $l$ に一致することを証明する。
$y^2=4px$ の両辺を $x$ で微分すると
\begin{align*}
&2y\dfrac{dy}{dx}=4p \\[4pt]
&\dfrac{dy}{dx}=\dfrac{2p}{y}
\end{align*}
であるから,$l$ の方向ベクトルを $\vec{l}$ とすると&2y\dfrac{dy}{dx}=4p \\[4pt]
&\dfrac{dy}{dx}=\dfrac{2p}{y}
\end{align*}
\begin{align*}
\vec{l}=(b,~2p)
\end{align*}
となる。\vec{l}=(b,~2p)
\end{align*}

$C$ の準線は $x=-p$ であり,焦点Fの座標は $(p,~0)$ である。また,準線と直線 $m$ の交点をPとすると
\begin{align*}
\Vec{PA}=(a+p,~0),~\Vec{FA}=(a-p,~b)
\end{align*}
$\mathrm{PA}=\mathrm{FA}$ であるから,$\Vec{PA}+\Vec{FA}$ は2直線 $m$, AFの二等分線と平行であり,成分を計算すると\Vec{PA}=(a+p,~0),~\Vec{FA}=(a-p,~b)
\end{align*}
\begin{align*}
\Vec{PA}+\Vec{FA}&=(a+p,~0)+(a-p,~b) \\[4pt]
&=(2a,~b)
\end{align*}
ここで,2つのベクトル $\vec{l}=(b,~2p)$ と $\Vec{PA}+\Vec{FA}=(2a,~b)$ において\Vec{PA}+\Vec{FA}&=(a+p,~0)+(a-p,~b) \\[4pt]
&=(2a,~b)
\end{align*}
\begin{align*}
b^2-2p\Cdota2a&=b^2-4pa \\[4pt]
&=0
\end{align*}
となるから,$\vec{l}$ と $\Vec{PA}+\Vec{FA}$ は平行であることが分かる。つまり,2直線 $l$, AFと接線 $l$ のなす角は等しいから,$x$ 軸に平行な光線が $C$ 上の点Aで反射したとき,反射光は必ず焦点Fを通る。b^2-2p\Cdota2a&=b^2-4pa \\[4pt]
&=0
\end{align*}

平面ベクトルの平行条件2つの平面ベクトル $\vec{a}=(p,~q)$, $\vec{b}=(r,~s)$ が平行であるとき
\begin{align*}
ps-qr=0
\end{align*}
が成り立つ。ps-qr=0
\end{align*}

ヒロ
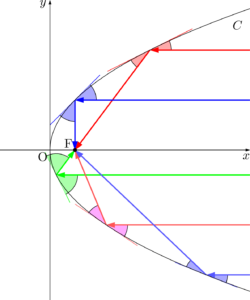
パラボラアンテナの焦点の位置に受信機を設置すると,パラボラアンテナの中心軸に平行に入射した電波は受信機にすべて同時に届くことになるね。

ヒロ
また,逆に焦点から信号を発信した場合は,パラボラアンテナの中心軸に平行な信号を送信することができるね。


















