Contents
放物線の性質に関する入試問題【2009年 北海道大】
2009年 北海道大$t>0$ とし,$x=t$ で表される直線を $l_1$ とする。$y=\dfrac{x^2}{4}$ で表される放物線を $C$ とおく。$C$ と $l_1$ の共有点 $\left(t,~\dfrac{t^2}{4}\right)$ における $C$ の接線を $l_2$ とする。このとき,以下の問いに答えよ。
(1) $l_1$ と $l_2$ のなす角を $\theta$ とするとき,$\cos\theta$ を求めよ。ただし,$0\leqq\theta\leqq\dfrac{\pi}{2}$ とする。
(2) $l_1$ を $l_2$ に関して対称移動させた直線を $l_3$ とおくとき,$l_3$ の方程式を求めよ。
(3) $l_3$ は $t$ によらない定点を通ることを示せ。
(4) $l_3$ と $C$ の2つの共有点をP, Qとする。線分PQの長さが最小になるような $t$ の値を求めよ。
(1) $l_1$ と $l_2$ のなす角を $\theta$ とするとき,$\cos\theta$ を求めよ。ただし,$0\leqq\theta\leqq\dfrac{\pi}{2}$ とする。
(2) $l_1$ を $l_2$ に関して対称移動させた直線を $l_3$ とおくとき,$l_3$ の方程式を求めよ。
(3) $l_3$ は $t$ によらない定点を通ることを示せ。
(4) $l_3$ と $C$ の2つの共有点をP, Qとする。線分PQの長さが最小になるような $t$ の値を求めよ。

ヒロ
とりあえず図を描いて状況を把握しよう。
【状況を把握するための図】
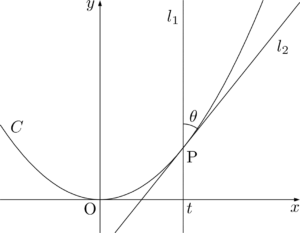


ヒロ
$\cos\theta$ を求める方法はいくつか考えられるけど,ベクトルを利用する解法でやってみよう。
【(1)の解答】
$y=\dfrac{x^2}{4}$ より
$y=\dfrac{x^2}{4}$ より
\begin{align*}
y’=\dfrac{x}{2}
\end{align*}
であるから,2直線 $l_1,~l_2$ の方向ベクトルを $\vec{l_1},~\vec{l_2}$ とするとy’=\dfrac{x}{2}
\end{align*}
\begin{align*}
\vec{l_1}=(0,~1),~\vec{l_2}=(2,~t)
\end{align*}
となる。また,\vec{l_1}=(0,~1),~\vec{l_2}=(2,~t)
\end{align*}
\begin{align*}
\abs{\vec{l_1}}=1,~\abs{\vec{l_2}}=\sqrt{t^2+4}
\end{align*}
であるから,求める $\cos\theta$ の値は次のようになる。\abs{\vec{l_1}}=1,~\abs{\vec{l_2}}=\sqrt{t^2+4}
\end{align*}
\begin{align*}
&\cos\theta=\dfrac{\vec{l_1}\Cdot\vec{l_2}}{\abs{\vec{l_1}}\abs{\vec{l_2}}} \\[4pt]
&\cos\theta=\dfrac{t}{\sqrt{t^2+4}}
\end{align*}
&\cos\theta=\dfrac{\vec{l_1}\Cdot\vec{l_2}}{\abs{\vec{l_1}}\abs{\vec{l_2}}} \\[4pt]
&\cos\theta=\dfrac{t}{\sqrt{t^2+4}}
\end{align*}

ヒロ
2直線のなす角についての問題では,$\tan$ を利用する解法で説明される場合が多いので,その方法でも解いておくよ。
【(1)の別解】
点Pにおける $C$ の接線 $l_2$ の傾きは $\dfrac{t}{2}$ であるから
点Pにおける $C$ の接線 $l_2$ の傾きは $\dfrac{t}{2}$ であるから
\begin{align*}
&\tan\left(\dfrac{\pi}{2}-\theta\right)=\dfrac{t}{2} \\[4pt]
&\tan\theta=\dfrac{2}{t}
\end{align*}
が成り立つ。$t>0$ のとき $\cos\theta>0$ であるから&\tan\left(\dfrac{\pi}{2}-\theta\right)=\dfrac{t}{2} \\[4pt]
&\tan\theta=\dfrac{2}{t}
\end{align*}
\begin{align*}
\cos\theta&=\dfrac{1}{\sqrt{1+\tan^2\theta}} \\[4pt]
&=\dfrac{1}{\sqrt{1+\left(\dfrac{2}{t}\right)^2}} \\[4pt]
&=\dfrac{t}{\sqrt{t^2+4}}
\end{align*}
\cos\theta&=\dfrac{1}{\sqrt{1+\tan^2\theta}} \\[4pt]
&=\dfrac{1}{\sqrt{1+\left(\dfrac{2}{t}\right)^2}} \\[4pt]
&=\dfrac{t}{\sqrt{t^2+4}}
\end{align*}

ヒロ
(2)をベクトルで考える場合は,正射影ベクトルについて理解していないとしんどいだろう。
【(1)の別解の続き】
$\vec{l_1}$ の $\vec{l_2}$ への正射影ベクトルを $\vec{m}$ とする。
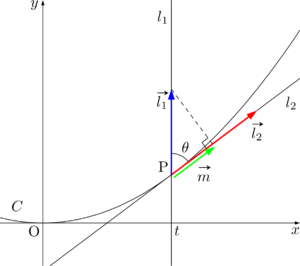
このとき
$\vec{l_1}$ の $\vec{l_2}$ への正射影ベクトルを $\vec{m}$ とする。

このとき
\begin{align*}
\vec{m}=\dfrac{\vec{l_1}\Cdot\vec{l_2}}{\abs{\vec{l_2}}^2}\vec{l_2}
\end{align*}
となる。$\vec{l_1}=(0,~1),~\vec{l_2}=(2,~t)$ より\vec{m}=\dfrac{\vec{l_1}\Cdot\vec{l_2}}{\abs{\vec{l_2}}^2}\vec{l_2}
\end{align*}
\begin{align*}
\vec{m}&=\dfrac{t}{t^2+4}(2,~t)
\end{align*}
ここで,直線 $l_3$ の方向ベクトルを $\vec{l_3}$ とすると\vec{m}&=\dfrac{t}{t^2+4}(2,~t)
\end{align*}
\begin{align*}
\dfrac{1}{2}(\vec{l_1}+\vec{l_3})=\vec{m}
\end{align*}
が成り立つから\dfrac{1}{2}(\vec{l_1}+\vec{l_3})=\vec{m}
\end{align*}
\begin{align*}
\vec{l_3}&=2\vec{m}-\vec{l_1} \\[4pt]
&=\dfrac{2t}{t^2+4}(2,~t)-(0,~1) \\[4pt]
&=\dfrac{1}{t^2+4}(4t,~t^2-4)
\end{align*}
よって,直線 $l_3$ は点Pを通り,傾き $\dfrac{t^2-4}{4t}$ の直線であるから,その方程式は次のようになる。\vec{l_3}&=2\vec{m}-\vec{l_1} \\[4pt]
&=\dfrac{2t}{t^2+4}(2,~t)-(0,~1) \\[4pt]
&=\dfrac{1}{t^2+4}(4t,~t^2-4)
\end{align*}
\begin{align*}
&y=\dfrac{t^2-4}{4t}(x-t)+\dfrac{t^2}{4} \\[4pt]
&y=\dfrac{t^2-4}{4t}x+1
\end{align*}
&y=\dfrac{t^2-4}{4t}(x-t)+\dfrac{t^2}{4} \\[4pt]
&y=\dfrac{t^2-4}{4t}x+1
\end{align*}

ヒロ
(1)を $\tan$ を用いて解いた場合は,(2)は次のように解くだろう。
【(2)の別解】
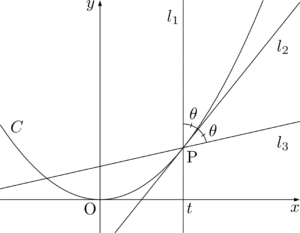
直線 $l_3$ は直線 $l_1$ となす角が $2\theta$ であるから,$l_3$ の傾きは

直線 $l_3$ は直線 $l_1$ となす角が $2\theta$ であるから,$l_3$ の傾きは
\begin{align*}
\tan\left(\dfrac{\pi}{2}-2\theta\right)&=\dfrac{1}{\tan2\theta} \\[4pt]
&=\dfrac{1-\tan^2\theta}{2\tan\theta} \\[4pt]
&=\dfrac{1-\left(\dfrac{2}{t}\right)^2}{2\Cdot\dfrac{2}{t}} \\[4pt]
&=\dfrac{t^2-4}{4t}
\end{align*}
\tan\left(\dfrac{\pi}{2}-2\theta\right)&=\dfrac{1}{\tan2\theta} \\[4pt]
&=\dfrac{1-\tan^2\theta}{2\tan\theta} \\[4pt]
&=\dfrac{1-\left(\dfrac{2}{t}\right)^2}{2\Cdot\dfrac{2}{t}} \\[4pt]
&=\dfrac{t^2-4}{4t}
\end{align*}

ヒロ
この後はさっきと同じだね。

ヒロ
直線が通る定点を求める問題といえば,恒等式の考え方だけど,今回は式を見れば一瞬で分かるから,すぐ答えを書いてしまって問題ない。
【(3)の解答】
(2)の結果より,$l_3$ は $t$ によらない定点 $(0,~1)$ を通る。
(2)の結果より,$l_3$ は $t$ によらない定点 $(0,~1)$ を通る。

ヒロ
$l_3$ と $C$ の方程式を連立して解くことでQの $x$ 座標を求めることができる。その後,$y$ 座標を求めれば,確かにPQの長さを求めることができる。

ヒロ
Pの $x$ 座標が $t$ であることを考えて因数分解しよう。
【(4)の解答】
$C:y=\dfrac{x^2}{4}$, $l_3:y=\dfrac{t^2-4}{4t}x+1$ より $y$ を消去すると
$C:y=\dfrac{x^2}{4}$, $l_3:y=\dfrac{t^2-4}{4t}x+1$ より $y$ を消去すると
\begin{align*}
&\dfrac{x^2}{4}=\dfrac{t^2-4}{4t}x+1 \\[4pt]
&tx^2-(t^2-4)x-4t=0 \\[4pt]
&(x-t)(tx+4)=0 \\[4pt]
&x=t,~-\dfrac{4}{t}
\end{align*}
よって,点Qの座標は $\left(-\dfrac{4}{t},~\dfrac{4}{t^2}\right)$ となる。&\dfrac{x^2}{4}=\dfrac{t^2-4}{4t}x+1 \\[4pt]
&tx^2-(t^2-4)x-4t=0 \\[4pt]
&(x-t)(tx+4)=0 \\[4pt]
&x=t,~-\dfrac{4}{t}
\end{align*}

ヒロ
この時点で2点P, Qの座標がそれぞれ $\left(t,~\dfrac{t^2}{4}\right)$, $\left(-\dfrac{4}{t},~\dfrac{4}{t^2}\right)$ と分かるけど,PQを計算するのはちょっと面倒だね。

ヒロ
この問題では,(3)で直線 $l_3$ が定点を通ることを示していて,放物線の性質を知っていれば,その定点は焦点であることが分かるよね。

ヒロ
ここで重要なのが,放物線の定義。

ヒロ
準線と焦点から等距離にある点の軌跡が放物線であることを考えると,PQの長さを簡単に求めることができる。
【(4)の解答の続き】
放物線 $C$ の焦点をFとすると,(3)で求めた定点はFであり,準線の方程式は $y=-1$ であることも分かる。
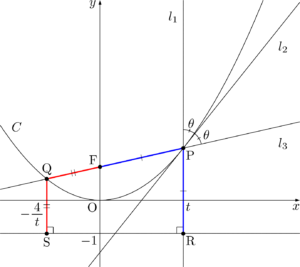
したがって,2点P, Qから準線に下ろした垂線の足をそれぞれR, Sとすると,放物線の定義より
よって,PQの長さが最小になる $t$ の値は $t=2$
放物線 $C$ の焦点をFとすると,(3)で求めた定点はFであり,準線の方程式は $y=-1$ であることも分かる。

したがって,2点P, Qから準線に下ろした垂線の足をそれぞれR, Sとすると,放物線の定義より
\begin{align*}
\mathrm{PF=PR},~\mathrm{QF=QS}
\end{align*}
なるから\mathrm{PF=PR},~\mathrm{QF=QS}
\end{align*}
\begin{align*}
\mathrm{PQ}&=\mathrm{PF+QF} \\[4pt]
&=\mathrm{PR+QS} \\[4pt]
&=\left(\dfrac{t^2}{4}+1\right)+\left(\dfrac{4}{t^2}+1\right) \\[4pt]
&=\dfrac{t^2}{4}+\dfrac{4}{t^2}+2
\end{align*}
$t^2>0$ であるから,相加・相乗平均の関係より\mathrm{PQ}&=\mathrm{PF+QF} \\[4pt]
&=\mathrm{PR+QS} \\[4pt]
&=\left(\dfrac{t^2}{4}+1\right)+\left(\dfrac{4}{t^2}+1\right) \\[4pt]
&=\dfrac{t^2}{4}+\dfrac{4}{t^2}+2
\end{align*}
\begin{align*}
\dfrac{t^2}{4}+\dfrac{4}{t^2}\geqq2\sqrt{\dfrac{t^2}{4}\Cdota\dfrac{4}{t^2}}=2
\end{align*}
等号が成り立つのは $\dfrac{t^2}{4}=\dfrac{4}{t^2}$,すなわち $t=2$ のときである。\dfrac{t^2}{4}+\dfrac{4}{t^2}\geqq2\sqrt{\dfrac{t^2}{4}\Cdota\dfrac{4}{t^2}}=2
\end{align*}
よって,PQの長さが最小になる $t$ の値は $t=2$
放物線の性質についてのまとめ

ヒロ
放物線の性質についてまとめると次のようになる。
放物線 $y^2=4px$
- グラフ
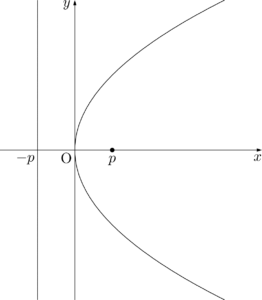
- 準線の方程式\begin{align*}
x=-p
\end{align*} - 焦点の座標\begin{align*}
(p,~0)
\end{align*} - 接線の方程式\begin{align*}
y_1y=2p(x+x_1)
\end{align*} - 媒介変数表示\begin{align*}
x=pt^2,~~y=2pt
\end{align*} - 極方程式\begin{align*}
r=\dfrac{2p}{1-\cos\theta}
\end{align*}
放物線 $x^2=4py$
- グラフ
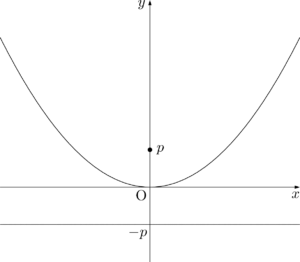
- 準線の方程式\begin{align*}
y=-p
\end{align*} - 焦点の座標\begin{align*}
(0,~p)
\end{align*} - 接線の方程式\begin{align*}
x_1x=2p(y+y_1)
\end{align*} - 媒介変数表示\begin{align*}
x=2pt,~~x=pt^2
\end{align*}


















