Contents
放物線の極方程式

ヒロ
放物線の極方程式を導出しよう。
焦点Fの座標を $\mathrm{F}(p,~0)$,準線の方程式を $x=-p$ とし,放物線 $C$ 上の点をPとする。また,PFと $x$ 軸の正の方向となす角を $\theta$ とする。
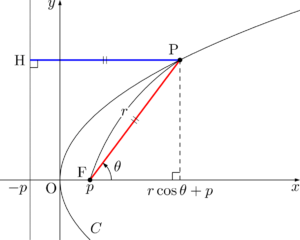
点Pから準線に下した垂線の足をHとすると,$\mathrm{PF}=\mathrm{PH}$ が成り立つから

点Pから準線に下した垂線の足をHとすると,$\mathrm{PF}=\mathrm{PH}$ が成り立つから
\begin{align*}
&r=(r\cos\theta+p)-(-p) \\[4pt]
&r=\dfrac{2p}{1-\cos\theta}
\end{align*}
&r=(r\cos\theta+p)-(-p) \\[4pt]
&r=\dfrac{2p}{1-\cos\theta}
\end{align*}

ヒロ
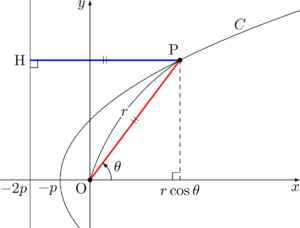
上の計算では,焦点Fからの距離を $r$ としたため,$r=\dfrac{2p}{1-\cos\theta}$ のグラフは次の図のようになる。焦点Fが原点の位置にくることに注意しよう。