2000年センター試験 数学ⅡB 第1問 複素数平面の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2000年 センターⅡB 第1問 複素数平面 $k$ を定数とし,$c$を正の定数とする。方程式
したがって,①の $-1$ 以外の解で,虚部(虚数単位 $i$ の係数)が正のものを $\alpha$ とすると
複素数平面において,原点をOとし,$\alpha$, $-1$ を表す点をそれぞれ A, B とする。三角形OABが二等辺三角形となるのは $c=\myBox{サ}$ のときである。このとき,$\alpha+1$ を極形式で表すと
\begin{align*}
x^3-kx^2+kcx+c^2=0~\cdots\cdots①
\end{align*}
を考える。方程式①が $x=-1$ を解にもつとする。このときx^3-kx^2+kcx+c^2=0~\cdots\cdots①
\end{align*}
\begin{align*}
k=\myBox{ア}-\myBox{イ}
\end{align*}
であり,①の左辺はk=\myBox{ア}-\myBox{イ}
\end{align*}
\begin{align*}
x^3-kx^2+kcx+c^2=(x+1)\left(x^2-\myBox{ウ}\,x+\myBox{エ}^{\myBox{オ}}\right)
\end{align*}
と因数分解される。x^3-kx^2+kcx+c^2=(x+1)\left(x^2-\myBox{ウ}\,x+\myBox{エ}^{\myBox{オ}}\right)
\end{align*}
したがって,①の $-1$ 以外の解で,虚部(虚数単位 $i$ の係数)が正のものを $\alpha$ とすると
\begin{align*}
\alpha=\myBox{カ}\left(\dfrac{\myBox{キ}}{\myBox{ク}}
+\dfrac{\sqrt{\myBox{ケ}}}{\myBox{コ}}i\right)
\end{align*}
となる。\alpha=\myBox{カ}\left(\dfrac{\myBox{キ}}{\myBox{ク}}
+\dfrac{\sqrt{\myBox{ケ}}}{\myBox{コ}}i\right)
\end{align*}
複素数平面において,原点をOとし,$\alpha$, $-1$ を表す点をそれぞれ A, B とする。三角形OABが二等辺三角形となるのは $c=\myBox{サ}$ のときである。このとき,$\alpha+1$ を極形式で表すと
\begin{align*}
\alpha+1=\sqrt{\myBox{シ}}\left(\cos\myBox{スセ}\Deg+i\sin\mybox{スセ}\Deg\right)
\end{align*}
であり,\alpha+1=\sqrt{\myBox{シ}}\left(\cos\myBox{スセ}\Deg+i\sin\mybox{スセ}\Deg\right)
\end{align*}
\begin{align*}
(\alpha+1)^6=\myBox{ソタチ}
\end{align*}
である。(\alpha+1)^6=\myBox{ソタチ}
\end{align*}
考え方と解答

ヒロ
方程式の解の意味を考えて解き進めよう。
【アイの解答】
$x=-1$ が①の解であるから
$x=-1$ が①の解であるから
\begin{align*}
&-1-k-kc+c^2=0 \\[4pt]
&(c+1)k-(c^2-1)=0 \\[4pt]
&(c+1)\{k-(c-1)\}=0
\end{align*}
$c>0$ のとき,$c+1\neq0$ であるから&-1-k-kc+c^2=0 \\[4pt]
&(c+1)k-(c^2-1)=0 \\[4pt]
&(c+1)\{k-(c-1)\}=0
\end{align*}
\begin{align*}
&k-(c-1)=0 \\[4pt]
&k=c-1
\end{align*}
&k-(c-1)=0 \\[4pt]
&k=c-1
\end{align*}

ヒロ
この結果,①の左辺が $x+1$ を因数にもつことが分かる。これを利用して因数分解しよう。
【ウ~オの解答】
\begin{align*}
&x^3-kx^2+kcx+c^2 \\[4pt]
&=x^3-(c-1)x^2+(c-1)cx+c^2 \\[4pt]
&=(x+1)(x^2-cx+c^2)
\end{align*}
&x^3-kx^2+kcx+c^2 \\[4pt]
&=x^3-(c-1)x^2+(c-1)cx+c^2 \\[4pt]
&=(x+1)(x^2-cx+c^2)
\end{align*}

ヒロ
次は①の解を求める問題。
【カ~コの解答】
①の $-1$ 以外の解は
①の $-1$ 以外の解は
\begin{align*}
x^2-cx+c^2=0
\end{align*}
の解である。これを解くとx^2-cx+c^2=0
\end{align*}
\begin{align*}
x&=\dfrac{c\pm\sqrt{c^2-4c^2}}{2} \\[4pt]
&=\dfrac{1\pm\sqrt{3}i}{2}c
\end{align*}
虚部が正のものが $\alpha$ であるからx&=\dfrac{c\pm\sqrt{c^2-4c^2}}{2} \\[4pt]
&=\dfrac{1\pm\sqrt{3}i}{2}c
\end{align*}
\begin{align*}
\alpha=c\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\right)
\end{align*}
\alpha=c\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\right)
\end{align*}

ヒロ
三角形OABが二等辺三角形になるような $c$ を求める問題。
【どの2辺が等しいかを考える】
2点O,Bは置いといて,点Aを考える。$\alpha=c\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\right)$ より
\begin{align*}
\abs{\alpha}=c,~\arg(\alpha)=60\Deg
\end{align*}
よって,次の図のように,点Aは半直線 $l$ 上にあることが分かる。\abs{\alpha}=c,~\arg(\alpha)=60\Deg
\end{align*}
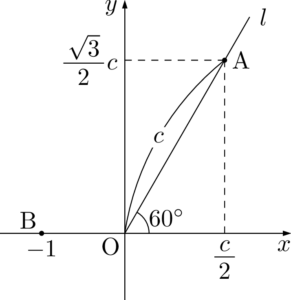
OAとABが等しくなることはない。また,OBとABも等しくなることはないと分かる。

ヒロ
これで解けるね。
【サの解答】
三角形OABが二等辺三角形になるのは,$\mathrm{OA}=\mathrm{OB}$ となるとき,すなわち $c=1$ のときである。
三角形OABが二等辺三角形になるのは,$\mathrm{OA}=\mathrm{OB}$ となるとき,すなわち $c=1$ のときである。

ヒロ
次は極形式で表す問題。
【シ~セの解答】
$c=1$ のとき,$\alpha=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$ であるから
$c=1$ のとき,$\alpha=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$ であるから
\begin{align*}
\alpha+1&=\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\right)+1 \\[4pt]
&=\dfrac{3}{2}+\dfrac{\sqrt{3}}{2}i \\[4pt]
&=\sqrt{3}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\[4pt]
&=\sqrt{3}(\cos30\Deg+i\sin30\Deg)
\end{align*}
\alpha+1&=\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\right)+1 \\[4pt]
&=\dfrac{3}{2}+\dfrac{\sqrt{3}}{2}i \\[4pt]
&=\sqrt{3}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\[4pt]
&=\sqrt{3}(\cos30\Deg+i\sin30\Deg)
\end{align*}

ヒロ
最後は複素数の累乗を求める問題だから,ド・モアブルの定理を利用しよう。
【ソ~チの解答】
ド・モアブルの定理より
ド・モアブルの定理より
\begin{align*}
(\alpha+1)^6&=(\sqrt{3})^6(\cos180\Deg+i\sin180\Deg) \\[4pt]
&=3^3\Cdota(-1) \\[4pt]
&=-27
\end{align*}
(\alpha+1)^6&=(\sqrt{3})^6(\cos180\Deg+i\sin180\Deg) \\[4pt]
&=3^3\Cdota(-1) \\[4pt]
&=-27
\end{align*}
2000年 センター数学ⅡB 複素数平面を解いた感想

ヒロ
前半の構成は1999年と似ていて,それほど難しい問題ではないだろう。

ヒロ
後半は三角形が二等辺三角形になるためにはどの2辺が等しいかをしっかり考えることが重要である。

ヒロ
最後の6乗を求める問題は,直前に極形式の形を求める問題になっているため,これも苦労しないだろう。