ベクトルの内積の図形的意味とは？

Contents

ページ1
1 ベクトルの内積の定義
ページ2
1 ベクトルの内積の図形的意味
ページ3
1 正射影ベクトル
2 点と直線の距離の公式の証明
3 ベクトルの内積の図形的意味についてのまとめ

正射影ベクトル

ヒロ

さっきの図において，$\Vec{OH}$ を $\vec{a},~\vec{b}$ で表したい場合は次のようにしよう。

$\abs{\vec{a}\Cdot\vec{b}}=\abs{\vec{a}}|\Vec{OH}|$ より

\begin{align*}
\Bigl|\Vec{OH}\Bigr|=\dfrac{\abs{\vec{a}\Cdot\vec{b}}}{\abs{\vec{a}}}
\end{align*}

ここで，分子の絶対値記号を外すと，OHの符号付き長さになるから，正射影ベクトル $\Vec{OH}$ は

\begin{align*}
\Vec{OH}&=\dfrac{\vec{a}\Cdot\vec{b}}{\abs{\vec{a}}}\cdot\dfrac{\vec{a}}{\abs{\vec{a}}} \\[4pt]
&=\dfrac{\vec{a}\Cdot\vec{b}}{\abs{\vec{a}}^2}\vec{a}
\end{align*}

と表すことができる。また，これより

\begin{align*}
\Vec{BH}&=\Vec{OH}-\Vec{OB} \\[4pt]
&=\dfrac{\vec{a}\Cdot\vec{b}}{\abs{\vec{a}}^2}\vec{a}-\vec{b}
\end{align*}

となるから，OAに垂直な方向のベクトルも，$\vec{a}$ と $\vec{b}$ で簡単に表すことができる。

点と直線の距離の公式の証明

ヒロ

それでは，ベクトルの内積の図形的意味を考えることで，点と直線の距離の公式の証明をしていくよ。

はい，お願いします！

下図のように，直線 $\ell:ax+by+c=0$ と点 $\mathrm{P}(x_0,y_0)$ との距離を $d$ とする。

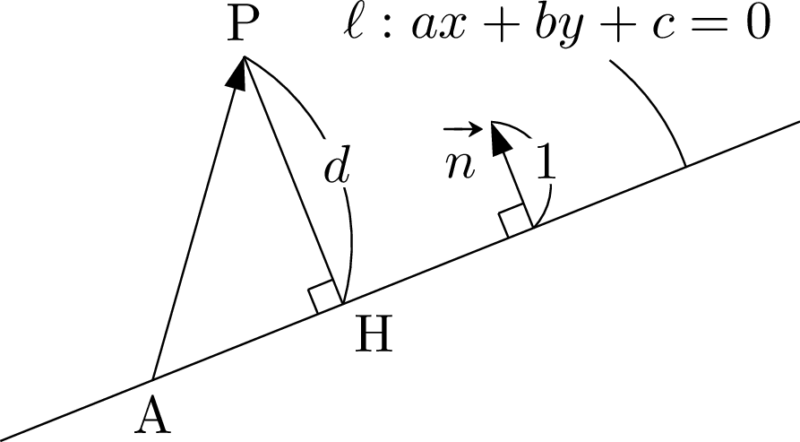
直線 $\ell$ の単位法線ベクトルを $\vec{n}$ とする。$|\vec{n}|=1$ であるから，$\overrightarrow{\mathrm{AP}}$ と $\vec{n}$ の内積の図形的意味を考えると，$d=\left|\vec{n}\Cdot\overrightarrow{\mathrm{AP}}\right|$ となる。

直線 $ax+by+c=0$ の法線ベクトル $\vec{n}$ は，$\vec{n}=(a,b)$ と表される。

光をどう当ててるのか分かりません。

ヒロ

照明を用意したよ。

PH と平行な直線AH$’$ を考え，スクリーンを直線 AH$’$ 上の $\vec{n}$ であると考える。

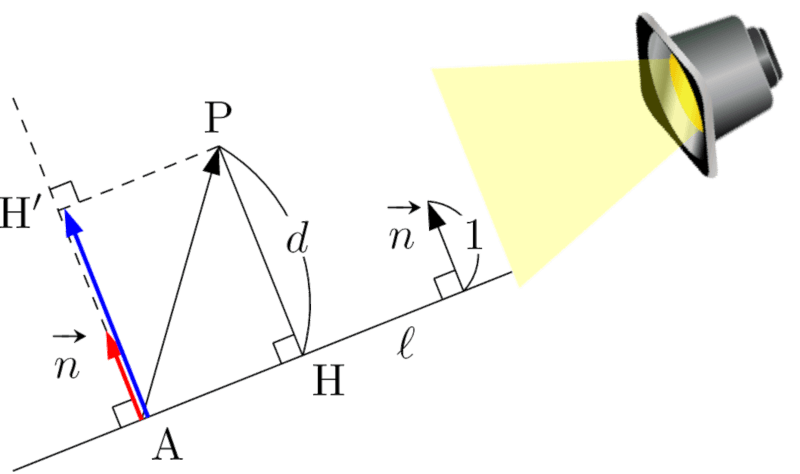
$\vec{n}$ をスクリーンとして，スクリーンに垂直な光を当てると，スクリーンからはみ出るけど，AP の影が AH$’$ となる。よって，$\left|\vec{n}\Cdot\overrightarrow{\mathrm{AP}}\right|
=|\vec{n}|\times\mathrm{AH}’$

$\mathrm{AH}’=\mathrm{HP}=d,|\vec{n}|=1$ より，$d=\left|\vec{n}\Cdot\overrightarrow{\mathrm{AP}}\right|$

なるほど！分かりました。

ヒロ

では，具体的に $d$ を求めていくよ。

直線 $\ell$ 上の点 A の座標を $(p,q)$ とすると，$ap+bq+c=0\ \cdots$ ①が成り立ち，$\overrightarrow{\mathrm{AP}}=(x_0-p,y_0-q)$ となる。また，$\displaystyle\vec{n}=\frac{1}{\sqrt{a^2+b^2}}(a,b)$ であるから，

\begin{align*}
d&=\left|\frac{1}{\sqrt{a^2+b^2}}(a,b)\Cdota(x_0-p,y_0-q)\right| \\[4pt]
&=\frac{|a(x_0-p)+b(y_0-q)|}{\sqrt{a^2+b^2}} \\[4pt]
&=\frac{|ax_0+by_0-(ap+bq)|}{\sqrt{a^2+b^2}}
\end{align*}

ここで，①より，$ap+bq=-c$ であるから，

\begin{align*}
d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}
\end{align*}