Contents
直線上の点の軌跡【明治薬科大】
2018年 明治薬科大$a$ を定数とする。$xy$ 平面上の点A$(3,~2)$ と直線 $l:x+(2a-1)y-8a+3=0$ に対し,Aから $l$ に下ろした垂線をAPとする。ただし,$l$ がAを通る場合は $\text{A}=\text{P}$ とする。
$l$ は $a$ の値にかかわらず定点 $\myhako$ を通り,$a$ が変化するときPの軌跡は中心が $\myhako$ で半径が $\myhako$ の円(ただし,$\myhako$ を除く)となる。したがって,線分APの長さの最大値は $\myhako$ である。
$l$ は $a$ の値にかかわらず定点 $\myhako$ を通り,$a$ が変化するときPの軌跡は中心が $\myhako$ で半径が $\myhako$ の円(ただし,$\myhako$ を除く)となる。したがって,線分APの長さの最大値は $\myhako$ である。
【考え方と解答】
直線 $l:x+(2a-1)y-8a+3=0$ の方程式を $a$ の方程式とみて整理すると
\begin{align*}
(2y-8)a+x-y+3=0\cdots\cdots①
\end{align*}
となる。これが $a$ の値にかかわらず成り立つのは(2y-8)a+x-y+3=0\cdots\cdots①
\end{align*}
\begin{align*}
\begin{cases}
2y-8=0 &\cdots\cdots② \\[4pt]
x-y+3=0 &\cdots\cdots③
\end{cases}
\end{align*}
が成り立つときである。②より,$y=4$\begin{cases}
2y-8=0 &\cdots\cdots② \\[4pt]
x-y+3=0 &\cdots\cdots③
\end{cases}
\end{align*}
③に代入して $x$ を求めると,$x=1$
よって,$l$ は $a$ の値にかかわらず定点 $(1,~4)$ を通る。
次に点Pの軌跡を求める。点Pは点Aを通り直線 $l$ に垂直な直線(直線 $m$ とする)と直線 $l$ との交点である。直線 $n$ の方程式は
\begin{align*}
&(2a-1)(x-3)-(y-2)=0 \\[4pt]
&(2a-1)x-y-6a+5=0 \\[4pt]
&(2x-6)a-x-y+5=0~\cdots\cdots④
\end{align*}
点Pの座標を求めるのが「主な目的」ではなく,点Pの軌跡を求めることが主な目的であるから,①と④から $a$ を消去して $x$ と $y$ の関係式を導こう。&(2a-1)(x-3)-(y-2)=0 \\[4pt]
&(2a-1)x-y-6a+5=0 \\[4pt]
&(2x-6)a-x-y+5=0~\cdots\cdots④
\end{align*}
$①\times(x-3)-④\times(y-4)$ より
\begin{align*}
&(x-y+3)(x-3)+(x+y-5)(y-4)=0 \\[4pt]
&x^2+y^2-4x-6y+11=0 \\[4pt]
&(x-2)^2+(y-3)^2=2
\end{align*}
この結果から,点Pは点$(2,~3)$ を中心とし,半径 $\sqrt{2}$ の円を描くことが分かる。しかし,解答を埋める空欄からも分かるように,点Pはこの円周上の点すべてを通るわけではないことが分かる。&(x-y+3)(x-3)+(x+y-5)(y-4)=0 \\[4pt]
&x^2+y^2-4x-6y+11=0 \\[4pt]
&(x-2)^2+(y-3)^2=2
\end{align*}
点Pが存在しないのは「点Aから直線 $l$ に垂線を下ろせない場合」であり,次の2つの場合が考えられる。
- 点Aから直線 $l$ 上にある
- 直線 $l$ が存在しない
まず,点Aから直線 $l$ 上にあるときは,点Aを点Pとすると問題文に書かれている。次に直線 $l$ の方程式をもう一度確認すると
\begin{align*}
x+(2a-1)y-8a+3=0
\end{align*}
となっているから,$x$ 軸に平行な直線を表せないことに気付く。直線 $l$ が定点$(1,~4)$ を通ることを考えると,直線 $l$ は直線 $y=4$ を表すことができない。点A$(3,~2)$ を通り $x$ 軸に垂直な直線の方程式は $x=3$ であるから,点Pは $(3,~4)$ と一致することはない。x+(2a-1)y-8a+3=0
\end{align*}
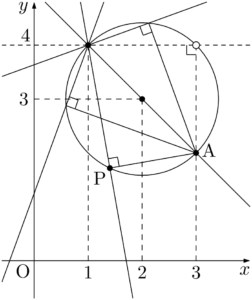
最後のAPの長さの最大値を求めよう。円周上の2点を結ぶ線分の長さが最大になるのは,その2点が直径の両端となるときである。つまり,APの長さが最大になるのは,点Pが$(1,~4)$ と一致したときであり,最大値は直径の $2\sqrt{2}$ である。

ヒロ
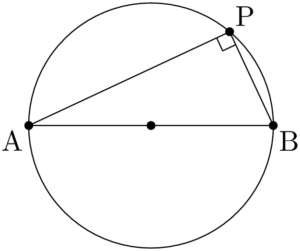
直径に対する円周角が $90\Deg$ であることは知っているだろう。

ヒロ
その逆の考え方も身に付けておくと良いだろう。
円を描く点2つの定点A,Bと1つの動点Pについて,$\kaku{APB}=90\Deg$ であるとき,点PはABを直径とする円を描く。ただし,2点A,Bを除く。


ヒロ
今回の問題では,定点B$(1,~4)$ を求めた時点で,$\kaku{APB}=90\Deg$ であることから,点PはABを直径とする円周上の点であることが分かる。


















