面積を求める6分の1公式について説明します。
6分の1公式を利用することで,定積分を簡単に計算することができます。
その結果,放物線と直線で囲まれた部分の面積や2つの放物線で囲まれた部分の面積を簡単に求めることができます。
どのようなときに6分の1公式を使えるのかを知って,正しく公式を使えるようにしましょう。
6分の1公式

ヒロ
6分の1公式とは次のような公式である。
6分の1公式
\begin{align*}
\dint{\alpha}{\beta}(x-\alpha)(x-\beta)\;dx=-\dfrac{1}{6}(\beta-\alpha)^3
\end{align*}
\dint{\alpha}{\beta}(x-\alpha)(x-\beta)\;dx=-\dfrac{1}{6}(\beta-\alpha)^3
\end{align*}

ヒロ
証明については,次の記事で解説しているため,この記事では省略する。

ヒロ
6分の1公式を用いて面積を求めるメリットは,被積分関数の $x^2$ の係数と2つの共有点の $x$ 座標が分かった時点で,すぐに面積を求めることができる点にある。
2021年 昭和薬科大
2021年 昭和薬科大放物線 $y=ax^2+bx+c~(a>0)$ は2点A$(-1,~8)$,B$(3,~0)$ を通り,放物線と線分ABで囲まれた部分の面積は $\dfrac{32}{3}$ である。このとき,$a=\myhako$,$b=\myhako$,$c=\myhako$ である。
【解答と考え方】
直線ABの方程式を $y=mx+n$ とすると,放物線と直線ABの交点は2点A,Bであることから,
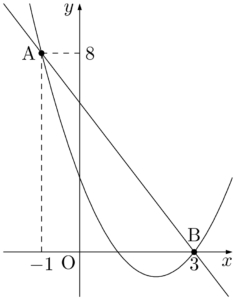
放物線は下に凸であるから,放物線と線分ABで囲まれた部分の面積 $S$ は次のようになる。
放物線 $y=x^2+bx+c$ が点Aを通るから
直線ABの方程式を $y=mx+n$ とすると,放物線と直線ABの交点は2点A,Bであることから,
\begin{align*}
ax^2+bx+c-(mx+n)=a(x+1)(x-3)
\end{align*}
と変形できる。直線ABの方程式を具体的に求めなくても,このように変形できることを理解しよう。一応,図示すると次のようになる。ax^2+bx+c-(mx+n)=a(x+1)(x-3)
\end{align*}

放物線は下に凸であるから,放物線と線分ABで囲まれた部分の面積 $S$ は次のようになる。
\begin{align*}
S&=-\dint{-1}{3}a(x+1)(x-3)\;dx \\[4pt]
&=\dfrac{1}{6}a\{3-(-1)\}^3 \\[4pt]
&=\dfrac{4^3}{6}a=\dfrac{32}{3}a
\end{align*}
これが $\dfrac{32}{3}$ に等しいからS&=-\dint{-1}{3}a(x+1)(x-3)\;dx \\[4pt]
&=\dfrac{1}{6}a\{3-(-1)\}^3 \\[4pt]
&=\dfrac{4^3}{6}a=\dfrac{32}{3}a
\end{align*}
\begin{align*}
&\dfrac{32}{3}a=\dfrac{32}{3} \\[4pt]
&a=1
\end{align*}
残りの $b,~c$ を求めるために,放物線が2点A,Bを通ることを利用しよう。&\dfrac{32}{3}a=\dfrac{32}{3} \\[4pt]
&a=1
\end{align*}
放物線 $y=x^2+bx+c$ が点Aを通るから
\begin{align*}
&1-b+c=8 \\[4pt]
&-b+c=7~\cdots\cdots①
\end{align*}
また,放物線が点Bを通るから&1-b+c=8 \\[4pt]
&-b+c=7~\cdots\cdots①
\end{align*}
\begin{align*}
&9+3b+c=0 \\[4pt]
&3b+c=-9~\cdots\cdots②
\end{align*}
①,②より,$b=-4,~c=3$&9+3b+c=0 \\[4pt]
&3b+c=-9~\cdots\cdots②
\end{align*}

ヒロ
今回の問題では,2点A,Bの座標が具体的に与えられているから,直線ABの方程式を求めて定積分の計算を行い,放物線と線分ABで囲まれた部分の面積を求めることができる。

ヒロ
しかし,直線ABの方程式を具体的に求めなくても,2点A,Bの $x$ 座標が分かっているから,6分の1公式を利用することで簡単に面積を求めることができる。

ヒロ
このことをしっかり理解して,面積を求められるようにしておきたい。
2021年 学習院大
2021年 学習院大$a$ を実数とし,2つの放物線
(1) $C_1$ と $C_2$ が異なる2点で交わるような $a$ の範囲を求めよ。
(2) $a$ が(1)で求めた範囲にあるとき,$C_1$ と $C_2$ とで囲まれた図形の面積を $S$ とする。$S$ を求めよ。
(3) $a$ が(1)で求めた範囲を動くとき,$S$ の最大値と,最大値を与える $a$ の値を求めよ。ただし,$S$ は(2)で求めた面積である。
\begin{align*}
C_1:y=x^2,~C_2:y=-x^2-2ax-2a^2+a
\end{align*}
を考える。C_1:y=x^2,~C_2:y=-x^2-2ax-2a^2+a
\end{align*}
(1) $C_1$ と $C_2$ が異なる2点で交わるような $a$ の範囲を求めよ。
(2) $a$ が(1)で求めた範囲にあるとき,$C_1$ と $C_2$ とで囲まれた図形の面積を $S$ とする。$S$ を求めよ。
(3) $a$ が(1)で求めた範囲を動くとき,$S$ の最大値と,最大値を与える $a$ の値を求めよ。ただし,$S$ は(2)で求めた面積である。
【(1)の解答と考え方】
$C_1$ と $C_2$ が異なる2点で交わるのは,$C_1,~C_2$ から $y$ を消去して得られる $x$ の2次方程式
$C_1$ と $C_2$ が異なる2点で交わるのは,$C_1,~C_2$ から $y$ を消去して得られる $x$ の2次方程式
\begin{align*}
2x^2+2ax+2a^2-a=0~\cdots\cdots①
\end{align*}
が異なる2つの実数解をもつときである。①の判別式を $D$ とすると,$D>0$ となるから2x^2+2ax+2a^2-a=0~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{D}{4}=a^2-2(2a^2-a)>0 \\[4pt]
&a(3a-2)<0 \\[4pt] &0<a<\dfrac{2}{3} \end{align*}
&\dfrac{D}{4}=a^2-2(2a^2-a)>0 \\[4pt]
&a(3a-2)<0 \\[4pt] &0<a<\dfrac{2}{3} \end{align*}
(2) $a$ が(1)で求めた範囲にあるとき,$C_1$ と $C_2$ とで囲まれた図形の面積を $S$ とする。$S$ を求めよ。
【(2)の解答と考え方】
$C_1,~C_2$ の2つの共有点の $x$ 座標は①の実数解である。しかし,解の公式を使うと①の実数解は次のような見た目が汚い式になる。
①の2つの解を $\alpha,~\beta~(\alpha<\beta)$ とおくと,解と係数の関係より
$C_1,~C_2$ の2つの共有点の $x$ 座標は①の実数解である。しかし,解の公式を使うと①の実数解は次のような見た目が汚い式になる。
\begin{align*} x=\dfrac{-a\pm\sqrt{-3a^2+2a}}{2} \end{align*}
この式を積分区間の上端・下端に書くのも嫌だし,定積分の計算で代入するのもやってられない気がするだろう。このように解の公式を使わないと得られない解が積分区間の端になる場合は,一旦 $\alpha,~\beta$ と文字でおいて,解と係数の関係を利用するのが良い。複雑な値を代入するときは,できるだけ簡単にしてから代入することが鉄則だからである。①の2つの解を $\alpha,~\beta~(\alpha<\beta)$ とおくと,解と係数の関係より
\begin{align*} \alpha+\beta=-a,~\alpha\beta=a^2-\dfrac{1}{2}a~\cdots\cdots② \end{align*}
$\alpha<x<\beta$ において,$C_2$ が $C_1$ の上側にあるから \begin{align*} S&=\dint{\alpha}{\beta}\{(-x^2-2ax-2a^2+a)-x^2\}\;dx \\[4pt] &=-2\dint{\alpha}{\beta}(x-\alpha)(x-\beta)\;dx \\[4pt] &=\dfrac{1}{3}(\beta-\alpha)^3 \end{align*}
ここまで計算すれば,$\beta-\alpha$ を求めることで $S$ を求めることができる。解の公式を使って具体的に解を求めても良いが,対称式の変形を利用して求める方法で説明しておく。\begin{align*} (\beta-\alpha)^2&=(\alpha+\beta)^2-4\alpha\beta \\[4pt] &=(-a)^2-4\left(a^2-\dfrac{1}{2}a\right) \\[4pt] &=-3a^2+2a \end{align*}
ここで「2乗を3乗にする変形」を覚えておこう。\begin{align*} (\beta-\alpha)^3=\{(\beta-\alpha)^2\}^{\frac{3}{2}} \end{align*}
上の式を利用することで $S$ は次のようになる。\begin{align*} S=\dfrac{1}{3}(-3a^2+2a)^{\frac{3}{2}} \end{align*}
(3) $a$ が(1)で求めた範囲を動くとき,$S$ の最大値と,最大値を与える $a$ の値を求めよ。ただし,$S$ は(2)で求めた面積である。
【(3)の解答と考え方】
(2)の結果より,$S$ が最大になるのは,$-3a^2+2a$ が最大のときであることが分かる。
(2)の結果より,$S$ が最大になるのは,$-3a^2+2a$ が最大のときであることが分かる。
\begin{align*} -3a^2+2a&=-3\left(a-\dfrac{1}{3}\right)^2+\dfrac{1}{3} \end{align*}
$0<a<\dfrac{2}{3}$ より,$a=\dfrac{1}{3}$ のとき,$-3a^2+2a$ は最大値 $\dfrac{1}{3}$ をとる。よって,$S$ の最大値は \begin{align*} \dfrac{1}{3}\left(\dfrac{1}{3}\right)^{\frac{3}{2}}&=\dfrac{1}{3}\Cdota\dfrac{1}{3\sqrt{3}}=\dfrac{\sqrt{3}}{27} \end{align*}

ヒロ
2次方程式の解と係数の関係については,次の記事で説明している。




















