Contents
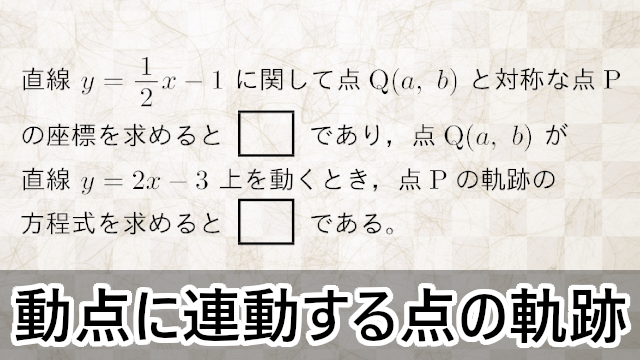
円周上の点と連動する点の軌跡【東京電機大】
2019年 東京電機大円 $C:x^2+y^2=1$ と点A$(4,~0)$ を考える。$C$ 上の点P$(p,~q)$ に対して,線分PAを $1:t~(t>0)$ に内分する点をQとする。Pが $C$ の周上を動くとき,Qの軌跡は円となり,それを $C’$ とする。このとき,次の問いに答えよ。
(1) 点Qの座標を $p,~q,~t$ を用いて表せ。
(2) 円 $C’$ の中心の座標と半径を,それぞれ $t$ を用いて表せ。
(3) $C$ と $C’$ がただ1つの共有点をもつとき,$t$ の値を求めよ。
(1) 点Qの座標を $p,~q,~t$ を用いて表せ。
(2) 円 $C’$ の中心の座標と半径を,それぞれ $t$ を用いて表せ。
(3) $C$ と $C’$ がただ1つの共有点をもつとき,$t$ の値を求めよ。

ヒロ
内分点については,次の記事を参考にしよう。
【(1)の考え方と解答】
点Qの座標を $(X,~Y)$ とおくと,点Qは線分PAを $1:t$ に内分する点であるから
点Qの座標を $(X,~Y)$ とおくと,点Qは線分PAを $1:t$ に内分する点であるから
\begin{align*}
\begin{cases}
X=\dfrac{tp+4}{t+1} &\cdots\cdots① \\[4pt]
Y=\dfrac{tq}{t+1} &\cdots\cdots②
\end{cases}
\end{align*}
よって,点Qの座標は $\left(\dfrac{tp+4}{t+1},~\dfrac{tq}{t+1}\right)$\begin{cases}
X=\dfrac{tp+4}{t+1} &\cdots\cdots① \\[4pt]
Y=\dfrac{tq}{t+1} &\cdots\cdots②
\end{cases}
\end{align*}
(2) 円 $C’$ の中心の座標と半径を,それぞれ $t$ を用いて表せ。
【(2)の考え方と解答】
①より $p=\dfrac{(t+1)X-4}{t}$
②より $q=\dfrac{t+1}{t}Y$
点Pは円 $C$ 上にあり $p^2+q^2=1$ が成り立つから
①より $p=\dfrac{(t+1)X-4}{t}$
②より $q=\dfrac{t+1}{t}Y$
点Pは円 $C$ 上にあり $p^2+q^2=1$ が成り立つから
\begin{align*}
&\left(\dfrac{(t+1)X-4}{t}\right)^2+\left(\dfrac{t+1}{t}Y\right)^2=1 \\[4pt]
&\left(X-\dfrac{4}{t+1}\right)^2+Y^2=\left(\dfrac{t}{t+1}\right)^2
\end{align*}
よって,円 $C’$ の中心は $\left(\dfrac{4}{t+1},~0\right)$,半径は $\dfrac{t}{t+1}$ である。&\left(\dfrac{(t+1)X-4}{t}\right)^2+\left(\dfrac{t+1}{t}Y\right)^2=1 \\[4pt]
&\left(X-\dfrac{4}{t+1}\right)^2+Y^2=\left(\dfrac{t}{t+1}\right)^2
\end{align*}
(3) $C$ と $C’$ がただ1つの共有点をもつとき,$t$ の値を求めよ。
【(3)の考え方と解答】
$C$ と $C’$ がただ1つの共有点をもつのは,2つの円が外接,または内接するときである。
(i) 外接するとき
中心間の距離が2つの円の半径の和と等しいから
中心間の距離が2つの円の半径の差と等しく,$\dfrac{t}{t+1}<=1$ であることに注意すると
$C$ と $C’$ がただ1つの共有点をもつのは,2つの円が外接,または内接するときである。
(i) 外接するとき
中心間の距離が2つの円の半径の和と等しいから
\begin{align*}
&\dfrac{4}{t+1}=1+\dfrac{t}{t+1} \\[4pt]
&4=(t+1)+t \\[4pt]
&t=\dfrac{3}{2}
\end{align*}
(ii) 内接するとき&\dfrac{4}{t+1}=1+\dfrac{t}{t+1} \\[4pt]
&4=(t+1)+t \\[4pt]
&t=\dfrac{3}{2}
\end{align*}
中心間の距離が2つの円の半径の差と等しく,$\dfrac{t}{t+1}<=1$ であることに注意すると
\begin{align*} &\dfrac{4}{t+1}=1-\dfrac{t}{t+1} \\[4pt] &4=(t+1)-t \\[4pt] &0\Cdot t=3 \end{align*}
これを満たす $t$ は存在しない。 以上より,求める $t$ の値は $t=\dfrac{3}{2}$