Contents
平面上の線分の内分点と外分点

ヒロ
それでは,平面上の線分の内分点について考えよう。
【平面上の線分の内分点の座標】
平面上の2点A$(a,~b)$,B$(c,~d)$について,ABを $m:n$ に内分する点をP$(p,~q)$とする。
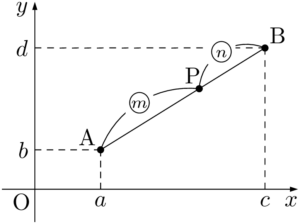
まず,点Pの $x$ 座標を求める。3点A, B, Pから $x$ 軸に下ろした垂線の足をそれぞれC,D,Hとすると,$\text{AC}$,$\text{PH}$,$\text{BD}$ はすべて平行であるから,$\text{CH}:\text{HD}=m:n$ である。
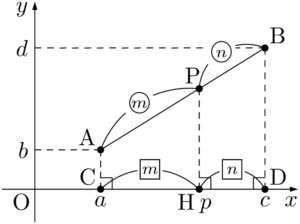
点HはCDを $m:n$ に内分する点であるから
\begin{align*}
p=\dfrac{na+mc}{m+n}
\end{align*}
点Pの $y$ 座標についても,$y$ 軸に垂線を下ろして同じように考えることでp=\dfrac{na+mc}{m+n}
\end{align*}
\begin{align*}
q=\dfrac{nb+md}{m+n}
\end{align*}
となることが分かるだろう。q=\dfrac{nb+md}{m+n}
\end{align*}
外分点については「言い換え」をすることで,数直線上の線分の外分点と同じように内分点として考えることができる。

ヒロ
以上をまとめると次のようになる。
平面上の線分の内分点と外分点平面上の2点A$(a,~b)$,B$(c,~d)$について,ABを $m:n$ に内分する点をP$(p,~q)$ とすると
\begin{align*}
p=\dfrac{na+mc}{m+n},~q=\dfrac{nb+md}{m+n}
\end{align*}
外分点については,「ABを $m:n$ に外分する」を「ABを $m:(-n)$ に内分する」か「ABを $(-m):n$ に内分する」に言い換えて内分点の式を利用しよう。p=\dfrac{na+mc}{m+n},~q=\dfrac{nb+md}{m+n}
\end{align*}
内分点の座標を求める問題
2004年 京都産業大座標平面上に,3点A$(1,~1)$,B$(4,~4)$,C$(0,~a)$ をとる。点Cより線分ABにおろした垂線をCHとする。点Hが線分ABを $1:2$ に内分するとき,実数 $a$ の値は $a=\myhako$ である。
【考え方と解答】
この問題で分かっていることは次の2つ。
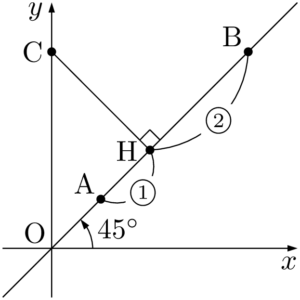
直線ABは $x$ 軸と45°の角をなし,原点を通る直線であるから,CHとABが垂直であるとき,$\sankaku{OCH}$ は直角二等辺三角形となるから,$\text{OC}=\sqrt{2}\text{OH}$ である。
この問題で分かっていることは次の2つ。
- CH$\perp$AB
- 点Hは線分ABを $1:2$ に内分する
それぞれから1本ずつ方程式を立てるとすると,未知数は2つまでにする必要がある。CH$\perp$ABから考えると,点Hの座標を文字でおいておく必要があるが,2つ目の条件から考えれば,点Hの座標を文字でおく必要がなく,ちょっとした計算で,$x$ 座標も $y$ 座標も求めることができる。ということで,まず,点Hの座標を求める。
点Hは線分ABを $1:2$ に内分する点であり,2点A,Bの $x$ 座標と $y$ 座標が等しいから,点Hの $x$ 座標と $y$ 座標は等しくなる。よって,
\begin{align*}
\dfrac{2\Cdot1+1\Cdot4}{1+2}=2
\end{align*}
より,点Hの座標はH$(2,~2)$ となる。\dfrac{2\Cdot1+1\Cdot4}{1+2}=2
\end{align*}

直線ABは $x$ 軸と45°の角をなし,原点を通る直線であるから,CHとABが垂直であるとき,$\sankaku{OCH}$ は直角二等辺三角形となるから,$\text{OC}=\sqrt{2}\text{OH}$ である。
\begin{align*}
\text{OH}=\sqrt{2^2+2^2}=2\sqrt{2}
\end{align*}
であるから\text{OH}=\sqrt{2^2+2^2}=2\sqrt{2}
\end{align*}
\begin{align*}
\text{OC}=\sqrt{2}\Cdota2\sqrt{2}=4
\end{align*}
したがって,$a=4$
\text{OC}=\sqrt{2}\Cdota2\sqrt{2}=4
\end{align*}

ヒロ
今回は「直角二等辺三角形」になる特殊な状態だったので,それをうまく利用して解いた。

ヒロ
しかし「垂直」ときたら,直線の傾きを利用することが多い気がする。

ヒロ
点Hの座標を求めた後,垂直条件を直線の傾きで考えると次のようになる。
【垂直条件を傾きで考える】
ABの傾きが1であるから,CHとABが垂直であるとき,CHの傾きは $-1$ である。よって
ABの傾きが1であるから,CHとABが垂直であるとき,CHの傾きは $-1$ である。よって
\begin{align*}
&\dfrac{2-a}{2-0}=-1 \\[4pt]
&2-a=-2 \\[4pt]
&a=4
\end{align*}
&\dfrac{2-a}{2-0}=-1 \\[4pt]
&2-a=-2 \\[4pt]
&a=4
\end{align*}


















