【数学ⅡB】内分点と外分点の座標【京都産業大】

Contents

数直線上の線分の外分点

ヒロ

次に外分点について理解しよう。

【外分点とは】
　例えば，数直線上の2点A(4)，B(7)について，$\text{AP}:\text{PB}=2:5$ となる線分AB上の点Pを考える。点PはABを $2:5$ の比に分ける点で，ABの外側にあるから「ABを $2:5$ に外分する点」と呼ばれる。いま，APとBPの長さの比から，点Pは点Bより点Aに近い側にあるから，点Aの左側にある。

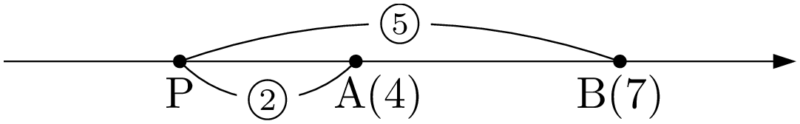
ABの長さに着目すると，比を表す数字を見て

\begin{align*}
\text{AB}=⑤-②=③
\end{align*}

となるから，$\text{AP}=\dfrac{2}{3}\text{AB}$ である。ここで，実際のABの長さは

\begin{align*}
\text{AB}=7-4=3
\end{align*}

であるから，

\begin{align*}
\text{AP}=\dfrac{2}{3}\Cdota3=2
\end{align*}

よって，点Pの座標は

\begin{align*}
(\text{P}の座標)&=(\text{A}の座標)-\text{AP} \\[4pt]
&=4-2=2
\end{align*}

ちなみに，もし $\text{AP}:\text{PB}=5:2$ となっていれば，点Pは点Bの右側にあることになる。

ヒロ

内分点と同じように，外分点についても一般化しよう。

【ABを $m:n$ の比に外分する点P】数直線上の2点A$(a)$，B$(b)~(a<b)$ について，ABを $m:n~(0<m<n)$ の比に内分する点P$(p)$ を考える。 $\text{AP}:\text{AB}=m:(n-m)$ であるから，APの長さは

\begin{align*} \text{AP}=\dfrac{m}{n-m}\text{AB}=\dfrac{m}{n-m}(b-a) \end{align*}

となる。よって

\begin{align*} p&=(\text{A}の座標)-\text{AP} \\[4pt] &=a-\dfrac{m}{n-m}(b-a) \\[4pt] &=\dfrac{na-mb}{n-m} \end{align*}

次に，$m$ と $n$ の大小関係を入れ換えた $0<n<m$ のときを考えてみよう。 $\text{AB}:\text{BP}=(m-n):n$ であるから，APの長さは

\begin{align*} \text{BP}=\dfrac{n}{m-n}\text{AB}=\dfrac{n}{m-n}(b-a) \end{align*}

となる。よって

\begin{align*} p&=(\text{B}の座標)+\text{BP} \\[4pt] &=b+\dfrac{n}{m-n}(b-a) \\[4pt] &=\dfrac{-na+mb}{m-n} \end{align*}

$0<m<n$ のときと $0<n<m$ のときの式をよく見ると，どちらも同じ式であることが分かる。最初に求めた $p$ の分母分子に $-1$ を掛けると確認できる。

\begin{align*} p=\dfrac{na-mb}{n-m}\times\dfrac{-1}{-1}=\dfrac{-na+mb}{m-n} \end{align*}

ヒロ

ということは，$m$ と $n$ の大小には関係なく，1つの式で外分点を求められるということである。

数直線上の線分の外分点数直線上の2点A$(a)$，B$(b)$ に対して，線分ABを $m:n$ に外分する点をPとすると，Pの座標は

\begin{align*} \dfrac{-na+mb}{m-n} \end{align*}

となる。ただし，$m>0,~n>0$ とする

負の比を利用することで外分を内分として計算する

ヒロ

数直線上の線分の内分点と外分点について説明したが，毎回導出なんてしてられないから，公式として覚えることになるだろう。

ヒロ

しかし，内分点と外分点で別々に公式を覚えるのは嫌という人は，外分点を内分点として処理する方法を知ると良いかもしれない。

【外分点を内分点として処理する方法】
　数直線上の2点A$(a)$，B$(b)$ に対して，線分ABを $m:n$ に外分する点Pの座標の見方を少し変えよう。

\begin{align*}
\dfrac{-na+mb}{m-n}=\dfrac{(-n)a+mb}{m+(-n)}
\end{align*}

と見ると，内分点の式において，$n$ を $-n$ にしたものであることが分かる。また，

\begin{align*}
\dfrac{na-mb}{n-m}=\dfrac{na+(-m)b}{n+(-m)}
\end{align*}

と見ることもできるため，内分点の式において，$m$ を $-m$ にしたものであると考えることもできる。
　つまり，「ABを $m:n$ に外分する」は「ABを $m:(-n)$ に内分する」や「ABを $(-m):n$ に内分する」と言い換えることができる。$m$ と $n$ のどちらにマイナスを付けるかについては，分母が正になるようにするのが良い。つまり「$m:n$ に外分する」を見たときに，$m$ の方が大きければ「$m:(-n)$ に内分する」と読み替えれば良いし，逆に $n$ の方が大きければ「$(-m):n$ に内分する」と読み替えれば良い。

ヒロ

ということで，この考え方を利用することで楽になることを願う。

外分点を内分点と見る「$m:n$ に外分する」は「$m:(-n)$ に内分する」か「$(-m):n$ に内分する」に読み替えることができる。