Contents
半角の公式の導出

ヒロ
それでは半角の公式を導出しよう。
$\cos2\alpha=1-2\sin^2\alpha$ より
\begin{align*}
\sin^2\alpha=\dfrac{1-\cos2\alpha}{2}
\end{align*}
ここで $\alpha=\dfrac{\theta}{2}$ とおくと\sin^2\alpha=\dfrac{1-\cos2\alpha}{2}
\end{align*}
\begin{align*}
\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}
\end{align*}
また,$\cos2\theta=2\cos^2\theta-1$ より\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}
\end{align*}
\begin{align*}
\cos^2\alpha=\dfrac{1+\cos2\alpha}{2}
\end{align*}
$\alpha=\dfrac{\theta}{2}$ とおくと\cos^2\alpha=\dfrac{1+\cos2\alpha}{2}
\end{align*}
\begin{align*}
\cos^2\dfrac{\theta}{2}=\dfrac{1+\cos\theta}{2}
\end{align*}
正弦・余弦の半角の公式より\cos^2\dfrac{\theta}{2}=\dfrac{1+\cos\theta}{2}
\end{align*}
\begin{align*}
&\tan^2\dfrac{\theta}{2}=\dfrac{\sin^2\dfrac{\theta}{2}}{\cos^2\dfrac{\theta}{2}} \\[4pt]
&\tan^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{1+\cos\theta}
\end{align*}
&\tan^2\dfrac{\theta}{2}=\dfrac{\sin^2\dfrac{\theta}{2}}{\cos^2\dfrac{\theta}{2}} \\[4pt]
&\tan^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{1+\cos\theta}
\end{align*}
2014年 関西大
2014年 関西大$\tan\alpha=-\dfrac{4}{3}$ かつ $0<\alpha<\pi$ であるとき,$\sin\alpha=\myhako$,$\cos\alpha=\myhako$ である。また,$\sin\dfrac{\alpha}{2}=\myhako$,$\cos\dfrac{\alpha}{2}=\myhako$ である。
【考え方と解答】
相互関係を利用して値を求めよう。サインとタンジェントの関係式を覚えていない人は覚えるようにしよう。
次に $\cos\alpha$ を求める。
同様に
相互関係を利用して値を求めよう。サインとタンジェントの関係式を覚えていない人は覚えるようにしよう。
\begin{align*} &\dfrac{1}{\sin^2\alpha}=1+\dfrac{1}{\tan^2\alpha} \\[4pt] &=1+\left(\dfrac{3}{4}\right)^2=\dfrac{25}{16} \\[4pt] \sin^2\alpha&=\dfrac{16}{25} \end{align*}
$0<\alpha<\pi$ のとき,$\sin\alpha>0$ であるから,$\sin\alpha=\dfrac{4}{5}$次に $\cos\alpha$ を求める。
\begin{align*}
\cos\alpha&=\dfrac{\sin\alpha}{\tan\alpha} \\[4pt]
&=\dfrac{4}{5}\Cdota\left(-\dfrac{3}{4}\right)=-\dfrac{3}{5}
\end{align*}
半角の公式を用いて $\sin\dfrac{\alpha}{2}$,$\cos\dfrac{\alpha}{2}$ を求めよう。\cos\alpha&=\dfrac{\sin\alpha}{\tan\alpha} \\[4pt]
&=\dfrac{4}{5}\Cdota\left(-\dfrac{3}{4}\right)=-\dfrac{3}{5}
\end{align*}
\begin{align*}
\sin^2\dfrac{\alpha}{2}&=\dfrac{1-\cos\alpha}{2} \\[4pt]
&=\dfrac{1+\dfrac{3}{5}}{2}=\dfrac{4}{5}
\end{align*}
$0<\dfrac{\alpha}{2}<\dfrac{\pi}{2}$ より,$\sin\dfrac{\alpha}{2}>0$ であるから,$\sin\dfrac{\alpha}{2}=\dfrac{2}{\sqrt{5}}$\sin^2\dfrac{\alpha}{2}&=\dfrac{1-\cos\alpha}{2} \\[4pt]
&=\dfrac{1+\dfrac{3}{5}}{2}=\dfrac{4}{5}
\end{align*}
同様に
\begin{align*}
\cos^2\dfrac{\alpha}{2}&=\dfrac{1+\cos\alpha}{2} \\[4pt]
&=\dfrac{1-\dfrac{3}{5}}{2}=\dfrac{1}{5}
\end{align*}
$0<\dfrac{\alpha}{2}<\dfrac{\pi}{2}$ より,$\cos\dfrac{\alpha}{2}>0$ であるから,$\cos\dfrac{\alpha}{2}=\dfrac{1}{\sqrt{5}}$\cos^2\dfrac{\alpha}{2}&=\dfrac{1+\cos\alpha}{2} \\[4pt]
&=\dfrac{1-\dfrac{3}{5}}{2}=\dfrac{1}{5}
\end{align*}
2019年 慶應義塾大
2019年 慶應義塾大関数
がある。$\theta$ が $0\leqq\theta\leqq\dfrac{\pi}{2}$ を満たすとき,この関数を $y=a\sin2\theta+b\cos2\theta+c$ で表すと,$a=\myhako$,$b=\myhako$,$c=\myhako$ となる。ただし,$a,~b,~c$ は三角関数を含まない実数とする。
がある。$\theta$ が $0\leqq\theta\leqq\dfrac{\pi}{2}$ を満たすとき,この関数を $y=a\sin2\theta+b\cos2\theta+c$ で表すと,$a=\myhako$,$b=\myhako$,$c=\myhako$ となる。ただし,$a,~b,~c$ は三角関数を含まない実数とする。
【考え方と解答】
半角の公式を利用して,角を $\theta$ から $2\theta$ に統一しよう。
半角の公式を利用して,角を $\theta$ から $2\theta$ に統一しよう。
\begin{align*}
y&=3\sqrt{3}\Cdota\dfrac{1-\cos2\theta}{2}+2\sqrt{3}\Cdota\dfrac{1+\cos2\theta}{2}+\dfrac{1}{2}\sin2\theta \\[4pt]
&=\dfrac{1}{2}\sin2\theta-\dfrac{\sqrt{3}}{2}\cos2\theta+\dfrac{5\sqrt{3}}{2}
\end{align*}
よって,y&=3\sqrt{3}\Cdota\dfrac{1-\cos2\theta}{2}+2\sqrt{3}\Cdota\dfrac{1+\cos2\theta}{2}+\dfrac{1}{2}\sin2\theta \\[4pt]
&=\dfrac{1}{2}\sin2\theta-\dfrac{\sqrt{3}}{2}\cos2\theta+\dfrac{5\sqrt{3}}{2}
\end{align*}
\begin{align*}
a=\dfrac{1}{2},~b=-\dfrac{\sqrt{3}}{2},~c=\dfrac{5\sqrt{3}}{2}
\end{align*}
a=\dfrac{1}{2},~b=-\dfrac{\sqrt{3}}{2},~c=\dfrac{5\sqrt{3}}{2}
\end{align*}
半角の公式を用いる最大最小問題
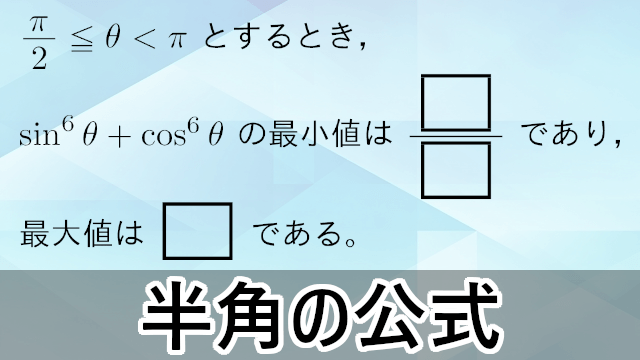
2018年 星薬科大$\dfrac{\pi}{2}\leqq\theta<\pi$ とするとき,$\sin^6\theta+\cos^6\theta$ の最小値は $\dfrac{\myhako}{\myhako}$ であり,最大値は $\myhako$ である。
【考え方と解答】
半角の公式を利用することで次数を下げることができる。一般に,次数が低いほど考えやすくなるから,半角の公式を使って次数を下げて考えよう。
半角の公式を利用することで次数を下げることができる。一般に,次数が低いほど考えやすくなるから,半角の公式を使って次数を下げて考えよう。
\begin{align*} &\sin^6\theta+\cos^6\theta \\[4pt] &=(\sin^2\theta+\cos^2\theta)^3-3\sin^2\theta\cos^2\theta(\sin^2\theta+\cos^2\theta) \\[4pt] &=1-3\sin^2\theta\cos^2\theta \\[4pt] &=1-3\Cdota\dfrac{1-\cos2\theta}{2}\Cdota\dfrac{1+\cos2\theta}{2} \\[4pt] &=1-\dfrac{3}{4}(1-\cos^22\theta) \\[4pt] &=\dfrac{1}{4}+\dfrac{3}{4}\Cdota\dfrac{1+\cos4\theta}{2} \\[4pt] &=\dfrac{3}{8}\cos4\theta+\dfrac{5}{8} \end{align*}
$\dfrac{\pi}{2}\leqq\theta<\pi$ のとき,$2\pi\leqq4\theta<4\pi$ であるから,$\sin^6\theta+\cos^6\theta$ が最小になるのは,$4\theta=3\pi$ すなわち $\theta=\dfrac{3}{4}\pi$ のときで最小値は \begin{align*} -\dfrac{3}{8}+\dfrac{5}{8}=\dfrac{1}{4} \end{align*}
である。$\sin^6\theta+\cos^6\theta$ が最大になるのは,$4\theta=2\pi$ すなわち $\theta=\dfrac{\pi}{2}$ のときで最大値は \begin{align*} \dfrac{3}{8}+\dfrac{5}{8}=1 \end{align*}
である。