2018年に筑波大で出題された三角関数の分数式の最大最小問題の3通りの解法について説明します。
色々な解法を考えることで,複数の単元の知識がリンクされるため,数学力の底上げにつながります。
2018年 筑波大$-\dfrac{2\pi}{3}\leqq\theta\leqq\dfrac{2\pi}{3}$ のとき,次式で示される $y$ の最大値および最小値を求めなさい。
\begin{align*}
y=\dfrac{1+\sin\theta}{1+\cos\theta}
\end{align*}
y=\dfrac{1+\sin\theta}{1+\cos\theta}
\end{align*}
プリントを次のリンクからダウンロードできます。
微分を用いる解法

ヒロ
数学IIIの三角関数の微分法と分数関数の微分法を学習済みなら,この解法で解くことができる。
$y=\dfrac{1+\sin\theta}{1+\cos\theta}$ より
\begin{align*}
y’&=\dfrac{\cos\theta(1+\cos\theta)-(1+\sin\theta)\Cdot(-\sin\theta)}{(1+\cos\theta)^2} \\[4pt]
&=\dfrac{1+\sin\theta+\cos\theta}{(1+\cos\theta)^2} \\[4pt]
&=\dfrac{1+\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)}{(1+\cos\theta)^2}
\end{align*}
$y’=0$ とするとy’&=\dfrac{\cos\theta(1+\cos\theta)-(1+\sin\theta)\Cdot(-\sin\theta)}{(1+\cos\theta)^2} \\[4pt]
&=\dfrac{1+\sin\theta+\cos\theta}{(1+\cos\theta)^2} \\[4pt]
&=\dfrac{1+\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)}{(1+\cos\theta)^2}
\end{align*}
\begin{align*}
&\sin\left(\theta+\dfrac{\pi}{4}\right)=-\dfrac{1}{\sqrt{2}}
\end{align*}
$-\dfrac{2\pi}{3}\leqq\theta\leqq\dfrac{2\pi}{3}$ より,&\sin\left(\theta+\dfrac{\pi}{4}\right)=-\dfrac{1}{\sqrt{2}}
\end{align*}
\begin{align*}
&\theta+\dfrac{\pi}{4}=-\dfrac{\pi}{4} \\[4pt]
&\theta=-\dfrac{\pi}{2}
\end{align*}
よって,$y$ の増減は次のようになる。&\theta+\dfrac{\pi}{4}=-\dfrac{\pi}{4} \\[4pt]
&\theta=-\dfrac{\pi}{2}
\end{align*}
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
\theta & -\dfrac{2\pi}{3} & \cdots & -\dfrac{\pi}{2} & \cdots & \dfrac{2\pi}{3} \\\hline
y’ & & – & 0 & + & \\\hline
y & 2-\sqrt{3} & \searrow & 0 & \nearrow & 2+\sqrt{3} \\\hline
\end{array}
\end{align*}
したがって,求める最大値と最小値は次のようになる。\begin{array}{|c||c|c|c|c|c|}\hline
\theta & -\dfrac{2\pi}{3} & \cdots & -\dfrac{\pi}{2} & \cdots & \dfrac{2\pi}{3} \\\hline
y’ & & – & 0 & + & \\\hline
y & 2-\sqrt{3} & \searrow & 0 & \nearrow & 2+\sqrt{3} \\\hline
\end{array}
\end{align*}
\begin{align*}
&最大値~~2+\sqrt{3}~\left(\theta=\dfrac{2\pi}{3}~のとき\right) \\[4pt]
&最小値~~0~(\theta=0~のとき)
\end{align*}
&最大値~~2+\sqrt{3}~\left(\theta=\dfrac{2\pi}{3}~のとき\right) \\[4pt]
&最小値~~0~(\theta=0~のとき)
\end{align*}
図形的意味を考える解法

ヒロ
三角関数の定義と分数式の図形的意味を考えよう。

ヒロ
$\cos\theta$ と $\sin\theta$ はそれぞれ原点を中心とする単位円周上の点の $x$ 座標と $y$ 座標を表している。

ヒロ
また,分数式を傾きとして捉えることで,単位円と直線の傾きの関係として考えることができるね。
$y=\dfrac{\sin\theta-(-1)}{\cos\theta-(-1)}$ であるから,$y$ は2点 $\mathrm{P}(\cos\theta,~\sin\theta)$, $\mathrm{A}(-1,~-1)$ を通る直線の傾きを表す。$-\dfrac{2\pi}{3}\leqq\theta\leqq\dfrac{2\pi}{3}$ より,点Pは原点を中心とする単位円周上の $x\geqq-\dfrac{1}{2}$ の部分(図の赤線部分)を動く。

図より,$y$ は $\theta=\dfrac{2\pi}{3}$ のとき最大となり,$\theta=-\dfrac{\pi}{2}$ のとき最小となる。
$\theta=\dfrac{2\pi}{3}$ のとき

図より,$y$ は $\theta=\dfrac{2\pi}{3}$ のとき最大となり,$\theta=-\dfrac{\pi}{2}$ のとき最小となる。
$\theta=\dfrac{2\pi}{3}$ のとき
\begin{align*}
y&=\dfrac{\dfrac{\sqrt3}{2}-(-1)}{-\dfrac{1}{2}-(-1)}=2+\sqrt3
\end{align*}
$\theta=-\dfrac{\pi}{2}$ のとき,$y=-1$y&=\dfrac{\dfrac{\sqrt3}{2}-(-1)}{-\dfrac{1}{2}-(-1)}=2+\sqrt3
\end{align*}
変数を変換する解法

ヒロ
三角関数の分数式を積分するときと同様に,$\tan\dfrac{\theta}{2}=t$ とおいてみよう。

ヒロ
変数変換した場合は,新しい変数の取り得る値の範囲に注意しよう。
$\tan\dfrac{\theta}{2}=t$ とおくと,$-\dfrac{2\pi}{3}\leqq\theta\leqq\dfrac{2\pi}{3}$ より,
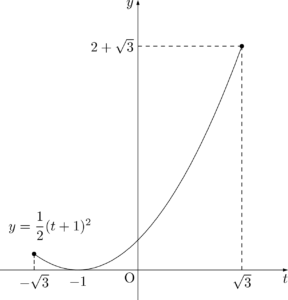
図より,$t=\sqrt3$ すなわち $\theta=\dfrac{2\pi}{3}$ のとき,$y$ は最大値 $2+\sqrt3$ をとることが分かる。また,$t=-1$ すなわち $\theta=-\dfrac{\pi}{2}$ のとき,$y$ は最小値 $0$ をとることが分かる。
\begin{align*}
-\sqrt3\leqq t\leqq\sqrt3
\end{align*}
となる。また,このとき-\sqrt3\leqq t\leqq\sqrt3
\end{align*}
\begin{align*}
&\cos\theta=\dfrac{1-t^2}{1+t^2} \\[4pt]
&\sin\theta=\dfrac{2t}{1+t^2}
\end{align*}
となるから,&\cos\theta=\dfrac{1-t^2}{1+t^2} \\[4pt]
&\sin\theta=\dfrac{2t}{1+t^2}
\end{align*}
\begin{align*}
y&=\dfrac{1+\dfrac{2t}{1+t^2}}{1+\dfrac{1-t^2}{1+t^2}} \\[4pt]
&=\dfrac{(1+t^2)+2t}{(1+t^2)+(1-t^2)} \\[4pt]
&=\dfrac{1}{2}(t+1)^2
\end{align*}
y&=\dfrac{1+\dfrac{2t}{1+t^2}}{1+\dfrac{1-t^2}{1+t^2}} \\[4pt]
&=\dfrac{(1+t^2)+2t}{(1+t^2)+(1-t^2)} \\[4pt]
&=\dfrac{1}{2}(t+1)^2
\end{align*}

図より,$t=\sqrt3$ すなわち $\theta=\dfrac{2\pi}{3}$ のとき,$y$ は最大値 $2+\sqrt3$ をとることが分かる。また,$t=-1$ すなわち $\theta=-\dfrac{\pi}{2}$ のとき,$y$ は最小値 $0$ をとることが分かる。
まとめ

ヒロ
今回は1つの問題を3通りの解法で解いたけど,解ける解法を1つ知ってれば良いというわけではない。

ヒロ
解けるなら複数の解法を学ぶ意味がないという人がいるが,合ってるとか間違ってるとかではなくて,勿体ない考え方だね。

ヒロ
1つの問題を見たときに,複数の解法が引き出せる人は,1つの解法しか引き出せない人より,多角的に物事を見ることができる。そのため,新しい考え方を知ったときにも受け入れやすく,自分のものにしやすい傾向がある。

ヒロ
こういうのを「性格」の一言で片付けず,色々な考え方を受け入れるようにすれば景色が変わるだろう。




















