ここでは2016年センター試験 数学ⅡB 第1問 指数関数・対数関数の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
(2) $y=2^x$ のグラフと $y=\left(\dfrac{1}{2}\right)^x$ のグラフは $\myBox{カ}$ である。
$y=2^x$ のグラフと $y=\log_2x$ のグラフは $\myBox{キ}$ である。
$y=\log_2x$ のグラフと $y=\log_{\frac{1}{2}}x$ のグラフは $\myBox{ク}$ である。
$y=\log_2x$ のグラフと $y=\log_2\dfrac{1}{x}$ のグラフは $\myBox{ケ}$ である。
$\myBox{カ}$ ~ $\myBox{ケ}$ に当てはまるものを,次の⓪~③のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
⓪ 同一のもの ① $x$ 軸に関して対称
② $y$ 軸に関して対称 ③ 直線 $y=x$ に関して対称
(3) $x>0$ の範囲における関数 $y=\left(\log_2\dfrac{x}{4}\right)^2-4\log_4x+3$ の最小値を求めよう。
$t=\log_2x$ とおく。このとき,$y=t^2-\myBox{コ}~t+\myBox{サ}$ である。また,$x$ が $x>0$ の範囲を動くとき,$t$ のとり得る値の範囲は $\myBox{シ}$ である。$\myBox{シ}$ に当てはまるものを,次の⓪~③のうちから一つ選べ。
⓪ $t>0$ ① $t>1$
② $t>0$ かつ $t\neq1$ ③ 実数全体
したがって,$y$ は $t=\myBox{ス}$ のとき,すなわち $x=\myBox{セ}$ のとき,最小値 $\myBox{ソタ}$ をとる。
(1)の解答

指数法則と対数法則を利用して計算しよう。
8^{\frac{5}{6}}&=(2^3)^{\frac{5}{6}} \\[4pt]
&=2^{\frac{5}{2}} \\[4pt]
&=4\sqrt{2}
\end{align*}
\log_{27}\dfrac{1}{9}&=\dfrac{\log_3\dfrac{1}{9}}{\log_327} \\[4pt]
&=\dfrac{-2}{3}
\end{align*}

対数とは何かを理解することもなく,対数法則を丸暗記して解く人がいるが,それを辞めると成績が上がること間違いなし!
次のような対数法則ガチガチの計算をしないようにしよう。
\log_{27}\dfrac{1}{9}&=\dfrac{\log_3\dfrac{1}{9}}{\log_327} \\[4pt]
&=\dfrac{\log_33^{-2}}{\log_33^3} \\[4pt]
&=\dfrac{-2\log_33}{3\log_33} \\[4pt]
&=-\dfrac{2}{3}
\end{align*}

例えば,$\log_3\dfrac{1}{9}$ は $3^x=\dfrac{1}{9}$ となる $x$ のことだと考えよう。すぐに $x=-2$ と分かるはずなので,$\log_3\dfrac{1}{9}=-2$ と書けるようにしよう。

$\log_{3}27$ も同様に考えて,27は3の何乗かを考えると,3の3乗だと分かるから,$\log_{3}27=3$ とすぐに書けるようにしよう。
(2)の解答
(2) $y=2^x$ のグラフと $y=\left(\dfrac{1}{2}\right)^x$ のグラフは $\myBox{カ}$ である。 $y=2^x$ のグラフと $y=\log_2x$ のグラフは $\myBox{キ}$ である。 $y=\log_2x$ のグラフと $y=\log_{\frac{1}{2}}x$ のグラフは $\myBox{ク}$ である。 $y=\log_2x$ のグラフと $y=\log_2\dfrac{1}{x}$ のグラフは $\myBox{ケ}$ である。 $\myBox{カ}$ ~ $\myBox{ケ}$ に当てはまるものを,次の⓪~③のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。 ⓪ 同一のもの ① $x$ 軸に関して対称 ② $y$ 軸に関して対称 ③ 直線 $y=x$ に関して対称

次はグラフの対称性に関する問題。
$f(x)=2^x$ とおくと
\left(\dfrac{1}{2}\right)^x=2^{-x}=f(-x)
\end{align*}
$y=a^x$ のグラフと $y=\log_ax$ のグラフは直線 $y=x$ に関して対称であるから,$\myBox{キ}=③$
$g(x)=\log_2x$ とおくと
\log_{\frac{1}{2}}x&=\log_2\dfrac{1}{x} \\[4pt]
&=-\log_2x \\[4pt]
&=-g(x)
\end{align*}
同様にして
\log_2\dfrac{1}{x}&=-\log_2x \\[4pt]
&=-g(x)
\end{align*}

対数の底と真数をそれぞれ累乗しても値が変わらない,すなわち次の等式を公式として知っておくと良い。

$n=-1$ のときは底と真数の両方の逆数をとることになり,$\log_ab=\log_{\frac{1}{a}}\dfrac{1}{b}$ が成り立つことは簡単に理解できる。
(3)の解答
(3) $x>0$ の範囲における関数 $y=\left(\log_2\dfrac{x}{4}\right)^2-4\log_4x+3$ の最小値を求めよう。 $t=\log_2x$ とおく。このとき,$y=t^2-\myBox{コ}~t+\myBox{サ}$ である。また,$x$ が $x>0$ の範囲を動くとき,$t$ のとり得る値の範囲は $\myBox{シ}$ である。$\myBox{シ}$ に当てはまるものを,次の⓪~③のうちから一つ選べ。 ⓪ $t>0$ ① $t>1$ ② $t>0$ かつ $t\neq1$ ③ 実数全体 したがって,$y$ は $t=\myBox{ス}$ のとき,すなわち $x=\myBox{セ}$ のとき,最小値 $\myBox{ソタ}$ をとる。

$y$ を $t$ で表す問題。
$t=\log_2x$ とおくとき
y&=\left(\log_2\dfrac{x}{4}\right)^2-4\log_4x+3 \\[4pt]
&=(\log_2x-2)^2-4\Cdota\dfrac{1}{2}\log_2x+3 \\[4pt]
&=(t-2)^2-2t+3 \\[4pt]
&=t^2-6t+7
\end{align*}

変数変換をしたときは,誘導にあるように新しく置いた文字の定義域を求めることを意識しよう。
$t=\log_2x$ とおくとき,$x$ が $x>0$ の範囲を動くと,$t$ は実数全体を動く。$\myBox{シ}=③$
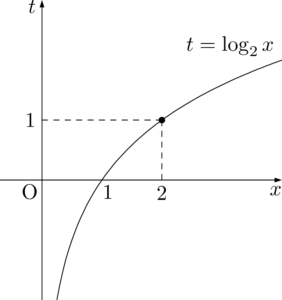

最後は2次関数の最小値を求める問題。
y&=t^2-6t+7 \\[4pt]
&=(t-3)^2-2
\end{align*}
このとき
&\log_2x=3 \\[4pt]
&x=2^3=8
\end{align*}
2016年 センター数学ⅡB 指数関数・対数関数を解いた感想

(1)は単純な計算問題だけど,計算時間を短くするためにも,指数法則や対数法則は丸暗記ではなく,意味を理解して使いこなせるようにすることが重要。

(2)は指数関数のグラフと対数関数のグラフの概形や関係を理解していないと得点するのは難しいだろう。

(3)は2次関数の最大最小問題に帰着させる問題なので,数学が苦手な人も点数を取りやすい問題かもしれない。





















