Contents
極値をもつ条件を求める問題
2020年 南山大関数 $f(x)=\dfrac{2}{3}x^3-ax^2+(a^2-16)x+2$ が極大値と極小値をもつとき,定数 $a$ のとりうる値の範囲は $\myBox{ア}$ である。また,極大値と極小値を与える $x$ の値がいずれも $x>0$ の範囲にあるとき,$a$ のとりうる値の範囲は $\myBox{イ}$ である。
【アの解答と考え方】
3次関数 $f(x)$ が極大値と極小値をもつのは,$f'(x)=0$ が異なる2つの実数解をもつときである。
3次関数 $f(x)$ が極大値と極小値をもつのは,$f'(x)=0$ が異なる2つの実数解をもつときである。
\begin{align*}
f'(x)=2x^2-2ax+a^2-16
\end{align*}
$f'(x)=0$ の判別式を $D$ とすると,$D>0$ となるからf'(x)=2x^2-2ax+a^2-16
\end{align*}
\begin{align*}
&\dfrac{D}{4}=a^2-2(a^2-16)>0 \\[4pt]
&-a^2+32>0 \\[4pt]
&-4\sqrt{2}<a<4\sqrt{2} \end{align*}
&\dfrac{D}{4}=a^2-2(a^2-16)>0 \\[4pt]
&-a^2+32>0 \\[4pt]
&-4\sqrt{2}<a<4\sqrt{2} \end{align*}
【イの考え方】
極大値と極小値を与える $x$ の値がいずれも $x>0$ の範囲にあるのは,$f'(x)=0$ が異なる2つの正の解をもつときである。2つの考え方がある。1つは $y=f'(x)$ のグラフと $x$ 軸が $x>0$ の範囲で異なる2つの共有点をもつ条件を考える方法。もう1つは,$f'(x)=0$ の2つの解を $\alpha,~\beta$ として,$\alpha>0$ かつ $\beta>0$ となる条件を解と係数の関係を利用して考える方法。
極大値と極小値を与える $x$ の値がいずれも $x>0$ の範囲にあるのは,$f'(x)=0$ が異なる2つの正の解をもつときである。2つの考え方がある。1つは $y=f'(x)$ のグラフと $x$ 軸が $x>0$ の範囲で異なる2つの共有点をもつ条件を考える方法。もう1つは,$f'(x)=0$ の2つの解を $\alpha,~\beta$ として,$\alpha>0$ かつ $\beta>0$ となる条件を解と係数の関係を利用して考える方法。

ヒロ
1つ目の考え方は「2次方程式の解の配置問題」の考え方であるため,苦手な人は次の記事で復習しておこう。
【イの解答と考え方】
1つ目の考え方の場合,判別式 $D$(頂点の $y$ 座標),軸,端点について考える。条件を満たすとき,$y=f'(x)$ のグラフは次のようになる。$y$ 切片と軸を求めて図に書き込んでいる。
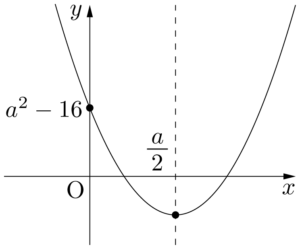
「$x$ 軸との共有点」を考えるのではなく,黒丸の2点($y$ 切片と頂点)について考えよう。
まず,頂点の $x$ 座標,つまり軸が $x>0$ の範囲になければならないから,
1つ目の考え方の場合,判別式 $D$(頂点の $y$ 座標),軸,端点について考える。条件を満たすとき,$y=f'(x)$ のグラフは次のようになる。$y$ 切片と軸を求めて図に書き込んでいる。

「$x$ 軸との共有点」を考えるのではなく,黒丸の2点($y$ 切片と頂点)について考えよう。
まず,頂点の $x$ 座標,つまり軸が $x>0$ の範囲になければならないから,
\begin{align*}
\dfrac{a}{2}>0~~\therefore a>0~\cdots\cdots①
\end{align*}
また,頂点の $y$ 座標が負でなければならない。これは判別式を $D$ とすると,$D>0$ と同じことを表している。計算しやすい方法で計算しよう。「判別式を $D$ とすると・・・」などダラダラ解答に書きたくない場合は,サクッと平方完成して,頂点の $y$ 座標を求めよう。今回は平方完成することにする。\dfrac{a}{2}>0~~\therefore a>0~\cdots\cdots①
\end{align*}
\begin{align*}
f'(x)=2\left(x-\dfrac{a}{2}\right)^2+\dfrac{1}{2}a^2-16
\end{align*}
となるから,頂点の $y$ 座標は $\dfrac{1}{2}a^2-16$ である。これが負であるからf'(x)=2\left(x-\dfrac{a}{2}\right)^2+\dfrac{1}{2}a^2-16
\end{align*}
\begin{align*}
&\dfrac{1}{2}a^2-16<0 \\[4pt] &a^2<32 \\[4pt] &-4\sqrt{2}<a<4\sqrt{2}~\cdots\cdots② \end{align*}
$y$ 切片が正であるから &\dfrac{1}{2}a^2-16<0 \\[4pt] &a^2<32 \\[4pt] &-4\sqrt{2}<a<4\sqrt{2}~\cdots\cdots② \end{align*}
\begin{align*} &a^2-16>0 \\[4pt]
&a<-4,~4<a~\cdots\cdots③ \end{align*}
①,②,③より,$4<a<4\sqrt{2}$&a<-4,~4<a~\cdots\cdots③ \end{align*}
【イの解答と考え方2】
2つ目の解と係数の関係を利用した解法を説明する。
$f'(x)=0$ の2つの解を $\alpha,~\beta$ とする。$f'(x)=0$ の判別式を $D$ とすると,$D>0$ となるから
2つ目の解と係数の関係を利用した解法を説明する。
$f'(x)=0$ の2つの解を $\alpha,~\beta$ とする。$f'(x)=0$ の判別式を $D$ とすると,$D>0$ となるから
\begin{align*}
&\dfrac{D}{4}=a^2-2(a^2-16)>0 \\[4pt]
&-a^2+32>0 \\[4pt]
&-4\sqrt{2}<a<4\sqrt{2}~\cdots\cdots① \end{align*}
また,解と係数の関係より &\dfrac{D}{4}=a^2-2(a^2-16)>0 \\[4pt]
&-a^2+32>0 \\[4pt]
&-4\sqrt{2}<a<4\sqrt{2}~\cdots\cdots① \end{align*}
\begin{align*} \alpha+\beta=a,~\alpha\beta=\dfrac{a^2-16}{2} \end{align*}
となる。$\alpha>0$ かつ $\beta>0$ のとき,\begin{align*}
\alpha+\beta>0~かつ~\alpha\beta>0
\end{align*}
となるから\alpha+\beta>0~かつ~\alpha\beta>0
\end{align*}
\begin{align*}
&a>0~かつ~a^2-16>0 \\[4pt]
&\therefore a>4~\cdots\cdots②
\end{align*}
①,②より,$4<a<4\sqrt{2}$&a>0~かつ~a^2-16>0 \\[4pt]
&\therefore a>4~\cdots\cdots②
\end{align*}

ヒロ
解と係数の関係についての知識があやふやな人は,次の記事を読んで知識を確実なものにしておこう。
3次関数が極値をもたない条件

ヒロ
それでは次に,3次関数が極値をもたない条件に関する知識を手に入れよう。

ヒロ
3次関数が極値をもたない条件は次のようになる。
極値をもたない条件3次関数 $f(x)$ が極値をもたない条件は,$D\leqq0$ である。ただし,$D$ は $f'(x)=0$ の判別式である。定義域が実数全体でない場合は,$f'(x)$ の符号が変化しない条件を考えるようにしよう。つまり,定義域内で $f'(x)=0$ が重解をもつか,実数解をもたない条件を考える。

ヒロ
極値をもつ条件を理解できていれば,極値をもたない条件も簡単に理解できるだろう。
説明は不要かもしれないが,一応説明しておく。
3次関数 $y=ax^3+bx^2+cx+d$ が極値をもたない条件を考える。
$f(x)=ax^3+bx^2+cx+d$ とする。3次関数 $f(x)$ が極値をもたないとき,$f'(x)=0$ となる $x$ が存在しない。つまり,$y=f'(x)$ のグラフが $x$ 軸と共有点をもたない。例えば $a>0$ のとき,$y=f'(x)$ のグラフが $x$ 軸と共有点をもたない状態を図示すると図3のようになる。
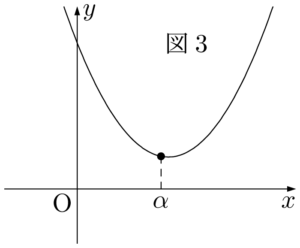
この状態を数式で表すと,$f'(\alpha)>0$ となる。ちなみに $f'(x)=0$ の判別式を $D$ とすると,$f'(\alpha)>0$ は $D<0$ とまったく同じ不等式になる。$f'(x)=0$ が実数解をもたないことを考えると,まったく同じ不等式になることも納得できるだろう。ただし,定義域が実数全体でない場合は,$f'(x)$ の符号が変化しない条件を考えるようにしよう。$a<0$ の場合も同様のことが言える。
3次関数 $y=ax^3+bx^2+cx+d$ が極値をもたない条件を考える。
$f(x)=ax^3+bx^2+cx+d$ とする。3次関数 $f(x)$ が極値をもたないとき,$f'(x)=0$ となる $x$ が存在しない。つまり,$y=f'(x)$ のグラフが $x$ 軸と共有点をもたない。例えば $a>0$ のとき,$y=f'(x)$ のグラフが $x$ 軸と共有点をもたない状態を図示すると図3のようになる。

この状態を数式で表すと,$f'(\alpha)>0$ となる。ちなみに $f'(x)=0$ の判別式を $D$ とすると,$f'(\alpha)>0$ は $D<0$ とまったく同じ不等式になる。$f'(x)=0$ が実数解をもたないことを考えると,まったく同じ不等式になることも納得できるだろう。ただし,定義域が実数全体でない場合は,$f'(x)$ の符号が変化しない条件を考えるようにしよう。$a<0$ の場合も同様のことが言える。
極値をもたない条件を求める問題
2020年 岡山理科大関数 $y=ax^3+x~(0<x<2)$ について,次の問いに答えよ。ただし,$a$ は定数とする。
(1) $a=-1$ のとき,この関数のグラフをかけ。
(2) この関数が極値をもたないような $a$ の値の範囲を求めよ。
(3) この関数の最大値が $\dfrac{1}{3}$ であるとき,$a$ の値を求めよ。また,最大値をとるときの $x$ の値を求めよ。
(1) $a=-1$ のとき,この関数のグラフをかけ。
(2) この関数が極値をもたないような $a$ の値の範囲を求めよ。
(3) この関数の最大値が $\dfrac{1}{3}$ であるとき,$a$ の値を求めよ。また,最大値をとるときの $x$ の値を求めよ。
【(1)の解答と考え方】
$a=-1$ のとき,$y=-x^3+x$
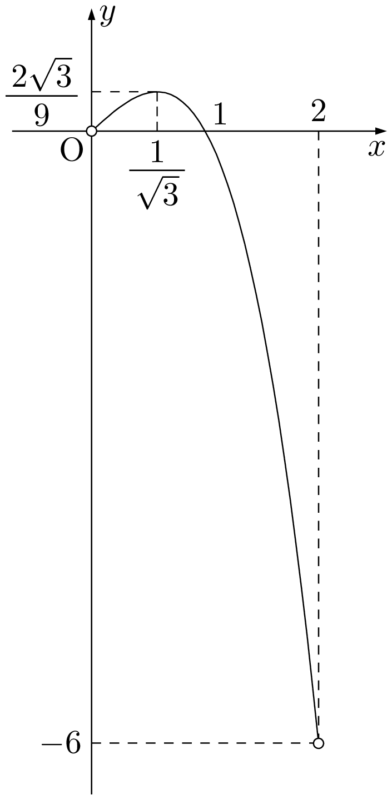
$a=-1$ のとき,$y=-x^3+x$
\begin{align*} y’=-3x^2+1 \end{align*}
$y’=0$ を解くと, \begin{align*} &x^2=\dfrac{1}{3} \\[4pt] &x=\pm\dfrac{1}{\sqrt{3}} \end{align*}
$0<x<2$ より,$x=\dfrac{1}{\sqrt{3}}$ \begin{align*} \begin{array}{|c||c|c|c|c|c|}\hline x & 0 & \cdots & \dfrac{1}{\sqrt{3}} & \cdots & 2 \\\hline f'(x) & & + & 0 & – & \\\hline f(x) & & \nearrow & & \searrow & \\\hline \end{array} \end{align*}
$x=\dfrac{1}{\sqrt{3}}$ のとき \begin{align*} f\left(\dfrac{1}{\sqrt{3}}\right)&=-\dfrac{1}{3\sqrt{3}}+\dfrac{1}{\sqrt{3}} \\[4pt] &=\dfrac{-1+3}{3\sqrt{3}}=-\dfrac{2\sqrt{3}}{9} \end{align*}
よって,グラフは次のようになる。
【(2)の解答と考え方】
この問題では,定義域が $0<x<2$ となっていることに注意しよう。定義域内で極値をもたないような $a$ の値の範囲を考える。つまり,$0<x<2$ において,$f'(x)$ の符号が変化しないような $a$ の値の範囲を求めればよいと分かる。
$f(x)=ax^3+1$ のとき,$f'(x)=3ax^2+1$
(i) $a\geqq0$ のとき,$0<x<2$ において $f'(x)$ の符号は変化しないから条件を満たす。
(ii) $a<0$ のとき,$f'(0)=1>0$ であるから,$0<x<2$ において $f'(x)$ の符号が変化しないのは,$f'(2)\geqq0$ となるときである。
(i),(ii)より,求める $a$ の値の範囲は,$a\geqq-\dfrac{1}{12}$
この問題では,定義域が $0<x<2$ となっていることに注意しよう。定義域内で極値をもたないような $a$ の値の範囲を考える。つまり,$0<x<2$ において,$f'(x)$ の符号が変化しないような $a$ の値の範囲を求めればよいと分かる。
$f(x)=ax^3+1$ のとき,$f'(x)=3ax^2+1$
(i) $a\geqq0$ のとき,$0<x<2$ において $f'(x)$ の符号は変化しないから条件を満たす。
(ii) $a<0$ のとき,$f'(0)=1>0$ であるから,$0<x<2$ において $f'(x)$ の符号が変化しないのは,$f'(2)\geqq0$ となるときである。
\begin{align*} &f'(2)=12a+1\geqq0 \\[4pt] &a\geqq-\dfrac{1}{12} \end{align*}
よって,$-\dfrac{1}{12}\leqq a<0$(i),(ii)より,求める $a$ の値の範囲は,$a\geqq-\dfrac{1}{12}$
【(3)の解答と考え方】
$a\geqq-\dfrac{1}{12}$ のとき,$0<x<2$ において $f(x)$ は増加するから最大値は存在しない。したがって,$a<-\dfrac{1}{12}$ のときを考える。$f'(x)=0$ を解くと,$x=\pm\sqrt{-\dfrac{1}{3a}}$ $0<x<2$ より,$x=\sqrt{-\dfrac{1}{3a}}$
$\sqrt{-\dfrac{1}{3a}}=\alpha$ とおくと,$f(x)$ の増減は次のようになる。
$a\geqq-\dfrac{1}{12}$ のとき,$0<x<2$ において $f(x)$ は増加するから最大値は存在しない。したがって,$a<-\dfrac{1}{12}$ のときを考える。$f'(x)=0$ を解くと,$x=\pm\sqrt{-\dfrac{1}{3a}}$ $0<x<2$ より,$x=\sqrt{-\dfrac{1}{3a}}$
$\sqrt{-\dfrac{1}{3a}}=\alpha$ とおくと,$f(x)$ の増減は次のようになる。
\begin{align*} \begin{array}{|c||c|c|c|c|c|}\hline x & 0 & \cdots & \alpha & \cdots & 2 \\\hline f'(x) & & + & 0 & – & \\\hline f(x) & & \nearrow & & \searrow & \\\hline \end{array} \end{align*}
したがって,$x=\alpha$ で $f(x)$ は極大かつ最大となる。このとき $\sqrt{-\dfrac{1}{3a}}=\alpha$ より\begin{align*} &-\dfrac{1}{3a}=\alpha^2 \\[4pt] &a\alpha^2=-\dfrac{1}{3} \end{align*}
であるから\begin{align*} f(\alpha)&=a\alpha^3+\alpha=a\alpha^2\Cdota\alpha+\alpha \\[4pt] &=-\dfrac{1}{3}\alpha+\alpha \\[4pt] &=\dfrac{2}{3}\alpha \end{align*}
最大値が $\dfrac{1}{3}$ のとき $f(\alpha)=\dfrac{1}{3}$ となるから\begin{align*} &\dfrac{2}{3}\alpha=\dfrac{1}{3} \\[4pt] &\alpha=\dfrac{1}{2} \\[4pt] &\alpha^2=\dfrac{1}{4} \\[4pt] &-\dfrac{1}{3a}=\dfrac{1}{4} \\[4pt] &a=-\dfrac{4}{3} \end{align*}




















