3次関数の極値とグラフについて説明します。
まずは関数の極値とは何かを知り,求め方を知りましょう。
さらに3次関数のグラフを描けるようにしましょう。
大学入試では,3次関数のグラフに関する様々な問題が出題されます。
Contents
関数の極大値と極小値

ヒロ
まず,極大と極大値について知ろう。
極大と極大値関数 $f(x)$ において,$x=a$ の付近で $f(a)\geqq f(x)$ が成り立つとき,$f(x)$ は $x=a$ で極大になるといい,$f(a)$ を極大値という。

ヒロ
ざっくりとした言い方をすると,山の頂上が極大ってこと。
【極大の例】
$x=a$ で極大となる例をいくつか挙げておこう。
次の図において,$x=a$ の前後で増加から減少に変わっていることが分かる。ちなみに $f'(a)=0$ である。
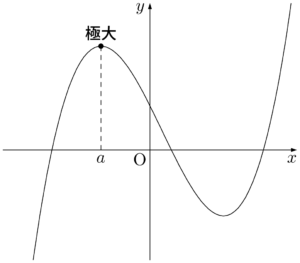
次の図でも,$x=a$ の前後で増加から減少に変わっている。上の図と異なるのは,$f'(a)$ は定義できない点である。
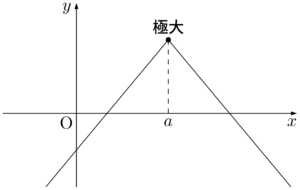
$x=a$ で極大となる例をいくつか挙げておこう。
次の図において,$x=a$ の前後で増加から減少に変わっていることが分かる。ちなみに $f'(a)=0$ である。

次の図でも,$x=a$ の前後で増加から減少に変わっている。上の図と異なるのは,$f'(a)$ は定義できない点である。


ヒロ
次に,極小と極小値について知ろう。
極小と極小値関数 $f(x)$ において,$x=a$ の付近で $f(a)\leqq f(x)$ が成り立つとき,$f(x)$ は $x=a$ で極小になるといい,$f(a)$ を極小値という。

ヒロ
ざっくりとした言い方をすると,谷の底が極小ってこと。
【極小の例】
$x=a$ で極小となる例をいくつか挙げておこう。
次の図において,$x=a$ の前後で減少から増加に変わっていることが分かる。ちなみに $f'(a)=0$ である。
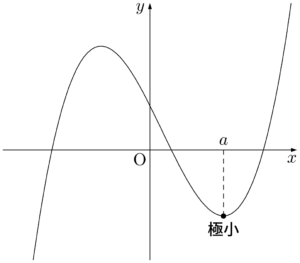
次の図でも,$x=a$ の前後で減少から増加に変わっている。上の図と異なるのは,$f'(a)$ は定義できない点である。
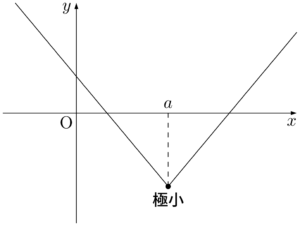
$x=a$ で極小となる例をいくつか挙げておこう。
次の図において,$x=a$ の前後で減少から増加に変わっていることが分かる。ちなみに $f'(a)=0$ である。

次の図でも,$x=a$ の前後で減少から増加に変わっている。上の図と異なるのは,$f'(a)$ は定義できない点である。



















