3次関数が極値をもつ条件と極値をもたない条件について説明します。
大学入試では,極値を求める問題以外に,極値をもつ条件や極値をもたない条件を求める問題が出題されることがよくあります。
様々な問題を解けるようにするために,1つずつ解ける問題を増やしていきましょう。
Contents
3次関数が極値をもつ条件

ヒロ
3次関数が極値をもつ条件を知ろう。
極値をもつ条件3次関数 $f(x)$ が極値をとるための必要十分条件は,$D>0$ である。ただし,$D$ は $f'(x)=0$ の判別式である。定義域が実数全体でない場合は,$f'(x)$ の符号が変化する条件を考える。つまり,定義域内で $f'(x)=0$ が異なる2つの実数解をもつ条件を考える。

ヒロ
次に,極値をもつ条件が上のようになる理由を知ろう。
3次関数 $y=ax^3+bx^2+cx+d$ が極値をもつ条件を考える。
$f(x)=ax^3+bx^2+cx+d$ とする。
$x=\alpha$ で極値をもつとすると,$f'(\alpha)=0$ が成り立つ。
$f'(x)=0$ の実数解は放物線 $y=f'(x)$ と $x$ 軸との交点の $x$ 座標である。$a>0$ とすると,$f'(x)=0$ が実数解をもつとき,$y=f'(x)$ のグラフは次の図1,2の2つの場合が考えられる。

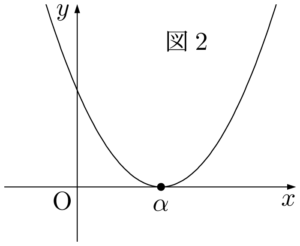
図1では,$x=\alpha$ の前後で $f'(x)$ の符号が正から負へ変わっているから,$x=\alpha$ で極大となることが分かる。また,$x=\beta$ の前後で $f'(x)$ の符号が負から正へ変わっているから,$x=\beta$ で極小となることが分かる。つまり,$f(x)$ が極値をとる条件を満たしている。
図2では,$x=\alpha$ の前後で $f'(x)$ の符号は正のまま変わらないから,$x=\alpha$ で極大にも極小にもならない。つまり,$f(x)$ が極値をとる条件を満たしていない。
$a<0$ の場合も同様のことが言えるから,3次関数 $f(x)$ が極値をとるための必要十分条件は,$f'(x)=0$ が異なる2つの実数解をもつことだと分かる。さらに話を進めると,2次方程式が異なる2つの実数解をもつとき,判別式を $D$ とすると,$D>0$ が成り立つから,3次関数 $f(x)$ が極値をとるための必要十分条件は,$f'(x)=0$ の判別式を $D$ とすると,$D>0$ であると言える。
ただし,定義域が実数全体でない場合は,$f'(x)$ の符号が変化する条件を考えるようにしよう。
$f(x)=ax^3+bx^2+cx+d$ とする。
$x=\alpha$ で極値をもつとすると,$f'(\alpha)=0$ が成り立つ。
\begin{align*}
f'(x)=3ax^2+2bx+c
\end{align*}
であるから,3次関数 $f(x)$ が極値をもつための条件は,$f'(x)=0$ が実数解(解を $x=\alpha$ とする)をもち,$x=\alpha$ の前後で $f'(x)$ の符号が変化することである。f'(x)=3ax^2+2bx+c
\end{align*}
$f'(x)=0$ の実数解は放物線 $y=f'(x)$ と $x$ 軸との交点の $x$ 座標である。$a>0$ とすると,$f'(x)=0$ が実数解をもつとき,$y=f'(x)$ のグラフは次の図1,2の2つの場合が考えられる。


図1では,$x=\alpha$ の前後で $f'(x)$ の符号が正から負へ変わっているから,$x=\alpha$ で極大となることが分かる。また,$x=\beta$ の前後で $f'(x)$ の符号が負から正へ変わっているから,$x=\beta$ で極小となることが分かる。つまり,$f(x)$ が極値をとる条件を満たしている。
図2では,$x=\alpha$ の前後で $f'(x)$ の符号は正のまま変わらないから,$x=\alpha$ で極大にも極小にもならない。つまり,$f(x)$ が極値をとる条件を満たしていない。
$a<0$ の場合も同様のことが言えるから,3次関数 $f(x)$ が極値をとるための必要十分条件は,$f'(x)=0$ が異なる2つの実数解をもつことだと分かる。さらに話を進めると,2次方程式が異なる2つの実数解をもつとき,判別式を $D$ とすると,$D>0$ が成り立つから,3次関数 $f(x)$ が極値をとるための必要十分条件は,$f'(x)=0$ の判別式を $D$ とすると,$D>0$ であると言える。
ただし,定義域が実数全体でない場合は,$f'(x)$ の符号が変化する条件を考えるようにしよう。


















