【数学ⅡB】放物線と直線で囲まれる2つの部分の面積が等しくなる条件【昭和大】

放物線と直線で囲まれる2つの部分の面積が等しくなる問題について説明します。

放物線が絡む図形の面積を求める際には，6分の1公式をうまく利用することを考えましょう。

その上で，放物線がもつ性質を知ることで計算量を減らすことができます。

しっかり解答を記述しないといけない試験であっても，答えをすぐに求められることで，記述で得た答えが合っていることを確認することができます。

「覚えても意味のないこと」や「知っても意味のないこと」なんて存在しないと考えて，知識を吸収しましょう。

2021年昭和大

2021年昭和大$m>1$ とする。$xy$ 平面において放物線 $y=mx-x^2~\cdots\cdots①$ と直線 $y=-x+m~\cdots\cdots②$ とがある。
(1) ①と②の交点の座標をすべて求めよ。
(2) ①と②で囲まれる図形の面積と，①と②および $y$ 軸とで囲まれる図形の面積が等しいとき，その面積を $S$ とする。そのときの $m$ の値と $S$ の値を求めよ。

【(1)の解答と考え方】
①，②より $y$ を消去すると

\begin{align*}
&mx-x^2=-x+m \\[4pt]&x^2-(m+1)x+m=0 \\[4pt]&(x-1)(x-m)=0 \\[4pt]&x=1,~m
\end{align*}

よって，求める交点の座標は $(1,~m-1),~(m,~0)$

(2) ①と②で囲まれる図形の面積と，①と②および $y$ 軸とで囲まれる図形の面積が等しいとき，その面積を $S$ とする。そのときの $m$ の値と $S$ の値を求めよ。

【(2)の解答と考え方】
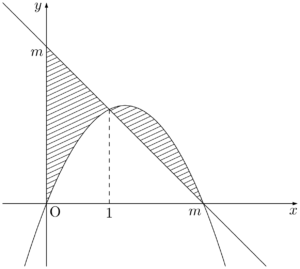
$S$ は下図の2つの斜線部分の面積の和の半分である。

答えだけ答えれば良い問題であれば，上の2つの斜線部分の面積が等しくなる条件を知っていればすぐに求めることができる。今回の問題の場合は，

\begin{align*}
&\dfrac{1}{3}m=1 \\[4pt]&m=3
\end{align*}

となる。また，このとき6分の1公式を用いて

\begin{align*}
S=\dfrac{1}{6}\Cdota2^3=\dfrac{4}{3}
\end{align*}

ヒロ

ここで，上の解答ではどのような知識を使ったのか説明しておく。

放物線の性質放物線 $C$ と $y$ 軸に平行でない直線 $l$ と $y$ 軸に平行な直線 $m$ を考える。$C$ と $l$ で囲まれた部分の面積を $S$，$C,~l,~m$ で囲まれた部分の面積を $T$ とする。

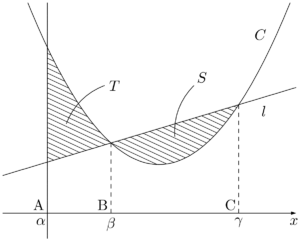
上図で，$S=T$ となるのは，$\mathrm{AB}:\mathrm{BC}=1:2$ のときである。

ヒロ

証明しておこう。

【証明】
$C$ を表す2次関数 $f(x)$ の $x^2$ の係数を $a~(>0)$ とする。また

\begin{align*}
\beta-\alpha=p,~\gamma-\beta=q
\end{align*}

とすると，6分の1公式を用いて

\begin{align*}
S&=\dfrac{1}{6}a(\gamma-\beta)^3 \\[4pt]&=\dfrac{1}{6}aq^3~\cdots\cdots①
\end{align*}

$l:y=g(x)$ とおくと，$C$ と $l$ の2つの交点の $x$ 座標が $\beta,~\gamma$ であることから

\begin{align*}
f(x)-g(x)=a(x-\beta)(x-\gamma)
\end{align*}

となる。よって，

\begin{align*}
T&=\dfrac{1}{2}\{f(\alpha)-g(\alpha)\}(\beta-\alpha)-\dfrac{1}{6}a(\beta-\alpha)^3 \\[4pt]&=\dfrac{1}{2}a(\alpha-\beta)(\alpha-\gamma)(\beta-\alpha)-\dfrac{1}{6}a(\beta-\alpha)^3 \\[4pt]&=\dfrac{1}{6}a(\beta-\alpha)^2\{3(\gamma-\alpha)-(\beta-\alpha)\} \\[4pt]&=\dfrac{1}{6}ap^2\{3(p+q)-p\} \\[4pt]&=\dfrac{1}{6}ap^2(2p+3q)~\cdots\cdots②
\end{align*}

$S=T$ のとき，①，②より

\begin{align*}
&q^3=p^2(2p+3q) \\[4pt]&q^3-3p^2q-2p^3=0 \\[4pt]&(q+p)^2(q-2p)=0
\end{align*}

$p+q\neq0$ であるから，$q=2p$
したがって，$\mathrm{AB}:\mathrm{BC}=1:2$ である。

ヒロ

この性質は，放物線が上に凸であっても成り立つ。また，2つの放物線と $y$ 軸に平行な直線で囲まれる2つの部分の面積が等しいときも成り立つ。

ヒロ

2021年の昭和大の問題は，記述式のため，解答をしっかり書く必要がある。

ヒロ

しかし，答えだけで良い穴埋め問題やマーク式試験では役に立つときもあるだろう。

【(2)の解答と考え方】
下図の2つの斜線部分の面積をそれぞれ $T_1,~T_2$ とする。

赤い補助線に注意して，6分の1公式を用いると

\begin{align*}
T_1&=\dfrac{1}{2}m-\dfrac{1}{6} \\[4pt]T_2&=\dfrac{1}{6}(m-1)^3
\end{align*}

$T_1=T_2$ のとき

\begin{align*}
&\dfrac{1}{2}m-\dfrac{1}{6}=\dfrac{1}{6}(m-1)^3 \\[4pt]&3m-1=m^3-3m^2+3m-1 \\[4pt]&m^3-3m^2=0 \\[4pt]&m^2(m-3)=0
\end{align*}

$m>1$ より，$m=3$
このとき，

\begin{align*}
S=\dfrac{1}{6}\Cdota2^3=\dfrac{4}{3}
\end{align*}

2021年 昭和大

2021年昭和大