Contents
- ページ1
- ページ2
- 1 直線が通過する領域とは
- ページ3
- 1 直線が通過する領域【東北大】
- ページ4
- 1 直線が通過する領域【早稲田大】
- ページ5
- 1 直線が通過する領域【横浜国立大】
直線が通過する領域【早稲田大】
2020年 早稲田大・改原点をOとする $xy$ 平面において,実数 $t$ に対して,直線
\begin{align*}
L:y=(2t-3)x-t^2+2
\end{align*}
を考える。直線 $L$ は,実数 $t$ の値によらず,放物線 $y=ax^2+bx+c$ の接線となる。このとき,定数 $a,~b,~c$ の値はL:y=(2t-3)x-t^2+2
\end{align*}
\begin{align*}
a=\myhako,~b=\myhako,~c=\myhako
\end{align*}
である。また,$t$ が $1\leqq t\leqq2$ を動くときに直線 $L$ が通過する領域のうち,$0\leqq x\leqq2$ の範囲にある部分を図示せよ。a=\myhako,~b=\myhako,~c=\myhako
\end{align*}
【考え方と解答】
微分を利用して解いても良いが,ここでは別の解法で説明する。放物線 $y=ax^2+bx+c$ を $C$ とすると,$C$ と $L$ が接するとき,二式から $y$ を消去して得られる $x$ の2次方程式は重解をもつことを利用する。$f(x)=(2t-3)x-t^2+2$ とおくと
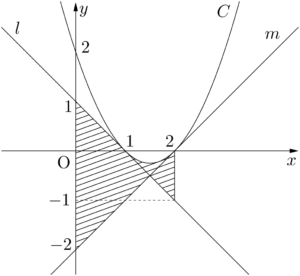
斜線部分のうち,$0\leqq x\leqq2$ の部分にある領域は下図の斜線部分となる。
微分を利用して解いても良いが,ここでは別の解法で説明する。放物線 $y=ax^2+bx+c$ を $C$ とすると,$C$ と $L$ が接するとき,二式から $y$ を消去して得られる $x$ の2次方程式は重解をもつことを利用する。$f(x)=(2t-3)x-t^2+2$ とおくと
\begin{align*}
&-3x+2-f(x)=t^2-2tx \\[4pt]
&-3x+2-f(x)=(t-x)^2-x^2 \\[4pt]
&x^2-3x+2-f(x)=(x-t)^2
\end{align*}
となる。これは放物線 $y=x^2-3x+2$ と直線 $y=f(x)$ が点 $(t,~f(t))$ で接することを表している。よって,&-3x+2-f(x)=t^2-2tx \\[4pt]
&-3x+2-f(x)=(t-x)^2-x^2 \\[4pt]
&x^2-3x+2-f(x)=(x-t)^2
\end{align*}
\begin{align*}
a=1,~b=-3,~c=2
\end{align*}
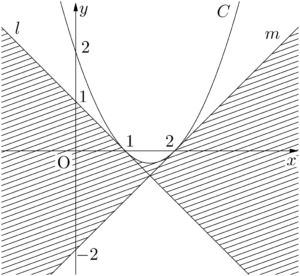
$t$ が $1\leqq t\leqq2$ を動くとき,直線 $L$ は放物線 $C:y=x^2-3x+2$ 上の $1\leqq x\leqq2$ の部分と接しながら動く。$t=1$ のとき,$f(x)=-x+1$ となり,$t=2$ のとき,$f(x)=x-2$ となる。$l:y=-x+1$,$m:y=-x+1$ とすると,直線 $L$ が通過する領域は下図の斜線部分(境界を含む)となる。a=1,~b=-3,~c=2
\end{align*}

斜線部分のうち,$0\leqq x\leqq2$ の部分にある領域は下図の斜線部分となる。


ヒロ
次のアニメーションは,直線 $L$ が放物線 $y=x^2-3x+2$ に接しながら動く様子である。


















