Contents
- ページ1
- ページ2
- 1 直線が通過する領域とは
- ページ3
- 1 直線が通過する領域【東北大】
- ページ4
- 1 直線が通過する領域【早稲田大】
- ページ5
- 1 直線が通過する領域【横浜国立大】
直線が通過する領域とは

ヒロ
まずは直線が通過する領域を求める基本的な考え方を知ろう。
【直線が通過する領域】
例として,直線 $l:tx+y+t^2=0~\cdots\cdots①$ が通過する領域を考える。ただし,$t$ はすべての実数をとり得るとする。実際に $t$ の値を色々変えると,直線 $l$ が動くことが分かる。
領域は点の集まりだから,具体的な点を考えて,直線 $l$ がその点を通るかどうか考えてみよう。
直線 $l$ が原点を通るかどうか調べる。①に $x=y=0$ を代入すると
\begin{align*}
t^2=0~~\therefore t=0
\end{align*}
これは,$t=0$ のときに直線 $l$ が原点を通ることを示している。別の点 $(0,~1)$ を通るかどうか調べよう。①に $x=0,~y=1$ を代入するとt^2=0~~\therefore t=0
\end{align*}
\begin{align*}
t^2+1=0
\end{align*}
となり,これをみたす実数 $t$ は存在しない。つまり,$t$ がどのような実数値をとっても,直線 $l$ が点 $(0,~1)$ を通ることはない。t^2+1=0
\end{align*}
このように,1つの点を通るかどうかを調べるだけなら簡単である。しかし,この考え方では,$l$ が通過する点をすべて求めることはできない。$l$ が通過する領域を求めるためには,考え方を変えなければならない。つまり,$l$ が通る点の座標を一般化して考える必要がある。$l$ が点 $(X,~Y)$ を通るとすると
\begin{align*}
&tX+y+t^2=0 \\[4pt]
&t^2+Xt+Y=0~\cdots\cdots②
\end{align*}
が成り立つ。$t$ の方程式②が実数解をもつとき,$l$ は点 $(X,~Y)$ を通るから,②が実数解をもつ条件を考える。判別式を $D$ とすると,$D\geqq0$ であるから&tX+y+t^2=0 \\[4pt]
&t^2+Xt+Y=0~\cdots\cdots②
\end{align*}
\begin{align*}
&X^2-4Y\geqq0 \\[4pt]
&Y\leqq\dfrac{1}{4}X^2
\end{align*}
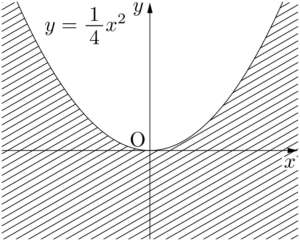
これは $l$ が通る点 $(X,~Y)$ は,放物線 $y=\dfrac{1}{4}x^2$ の下側(放物線上の点を含む)にあることを示している。つまり,直線 $l$ が通過する領域は,放物線 $y=\dfrac{1}{4}x^2$ の下側である。&X^2-4Y\geqq0 \\[4pt]
&Y\leqq\dfrac{1}{4}X^2
\end{align*}

ヒロ
この結果を踏まえて,直線 $l$ が動く様子を見ると,$l$ が放物線 $y=\dfrac{1}{4}x^2$ に接しながら動いていることが分かるだろう。

ヒロ
この問題において,放物線 $y=\dfrac{1}{4}x^2$ は直線 $l$ の「包絡線」と呼ばれる曲線である。

ヒロ
包絡線については,次の記事で説明しているので気になる人は参考にすると良いだろう。

ヒロ
一般に次のことがいえる。
直線 $f(x,~y,~t)=0$ が点 $(X,~Y)$ を通るとき
\begin{align*}
f(X,~Y,~t)=0~\cdots\cdots①
\end{align*}
が成り立つ。これは①を $t$ の方程式とみたとき,①をみたす実数 $t$ が存在すると言い換えることができる。つまり,方程式①をみたす実数 $t$ が存在するような点 $(X,~Y)$ の集合が直線 $f(x,~y,~t)=0$ が通過する領域である。f(X,~Y,~t)=0~\cdots\cdots①
\end{align*}



















