【数学ⅡB】直線が通過する領域【東北大・早稲田大・横浜国立大】

Contents

直線が通過する領域【横浜国立大】

2019年横浜国立大Oを原点とする $xy$ 平面上に2点A$(2,~0)$，B$(0,~2)$ がある。2点P，Qは条件(＊)をみたしながら動く。

\begin{align*}
(*)\begin{cases}
\text{Pは線分OA上にある。} \\[4pt]\text{Qは線分OB上にある。} \\[4pt]\sankaku{OPQ}\text{の面積は1である。}
\end{cases}
\end{align*}

点Pの座標を $(t,~0)$ とする。次の問いに答えよ。
(1) $t$ のとり得る値の範囲を求めよ。
(2) $t$ が(1)で求めた範囲を動くとき，線分PQが通過する領域を $xy$ 平面上に図示せよ。

【(1)の考え方と解答】
　点Pは線分OA上にあるから，$0<=t\leqq2~\cdots\cdots①$ また，点Qの座標を $(s,~0)$ とおくと，$\sankaku{OPQ}$ の面積が1であることから

\begin{align*} &\dfrac{1}{2}st=1 \\[4pt] &s=\dfrac{2}{t} \end{align*}

点Qは線分OB上にあるから

\begin{align*} &0<=s\leqq2 \\[4pt] &0<=\dfrac{2}{t}<=2 \\[4pt] &1\leqq t~\cdots\cdots② \end{align*}

①，②より，$1\leqq t\leqq2$

(2) $t$ が(1)で求めた範囲を動くとき，線分PQが通過する領域を $xy$ 平面上に図示せよ。

【(2)の考え方と解答】
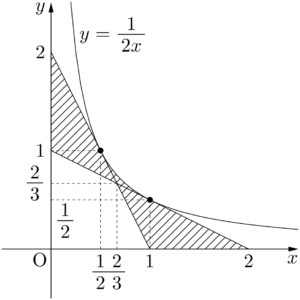
　2点P，Qの座標はP$(t,~0)$，Q$\left(0,~\dfrac{2}{t}\right)$ であるから，直線PQの方程式は

\begin{align*} &\dfrac{x}{t}+\dfrac{y}{\dfrac{2}{t}}=1 \\[4pt] &2x+t^2y-2t=0~\cdots\cdots③ \end{align*}

③を $t$ の方程式とみて変形すると

\begin{align*} yt^2-2t+2x=0~\cdots\cdots④ \end{align*}

④をみたす実数 $t$ が存在するための条件は，判別式を $D$ とすると，$D\geqq0$ であるから

\begin{align*} &\dfrac{D}{4}=1-2xy\geqq0 \\[4pt] &y\leqq\dfrac{1}{2x} \end{align*}

$y=\dfrac{1}{2x}$ のとき，④は重解 $t=\dfrac{1}{y}=2x$ をもつ。これは直線③と双曲線④が $x$ 座標が $\dfrac{t}{2}$ の点で接することを表している。
　$1\leqq t\leqq2$ のとき，接点は双曲線④の $\dfrac{1}{2}\leqq x\leqq1$ の部分を動く。また，直線③の方程式は $t=1$ のとき $2x+y-2=0$ となり，$t=2$ のとき $x+2y-2=0$ である。
　よって，求める線分PQが通過する領域は下図の斜線部分（境界を含む）となる。

ヒロ

次のアニメーションを見ることで，線分PQが動く様子を確認することができる。