Contents
- ページ1
- ページ2
- 1 直線が通過する領域とは
- ページ3
- 1 直線が通過する領域【東北大】
- ページ4
- 1 直線が通過する領域【早稲田大】
- ページ5
- 1 直線が通過する領域【横浜国立大】
直線が通過する領域【東北大】
2018年 東北大$xy$ 平面における2つの放物線 $C:y=(x-a)^2+b$,$D:y=-x^2$ を考える。
(1) $C$ と $D$ が異なる2点で交わり,その2交点の $x$ 座標の差が1となるように実数 $a,~b$ が動くとき,$C$ の頂点 $(a,~b)$ の軌跡を図示せよ。
(2) 実数 $a,~b$ が(1)の条件を満たしながら動くとき,$C$ と $D$ の2交点を結ぶ直線が通過する領域を求め,図示せよ。
(1) $C$ と $D$ が異なる2点で交わり,その2交点の $x$ 座標の差が1となるように実数 $a,~b$ が動くとき,$C$ の頂点 $(a,~b)$ の軌跡を図示せよ。
(2) 実数 $a,~b$ が(1)の条件を満たしながら動くとき,$C$ と $D$ の2交点を結ぶ直線が通過する領域を求め,図示せよ。
【(1)の考え方と解答】
$C:y=(x-a)^2+b$,$D:y=-x^2$ より $y$ を消去すると
$C$ と $D$ の2交点の $x$ 座標の差が1であるから,①の2解を $\alpha,~\alpha+1$ とおくと,解と係数の関係より
$C:y=(x-a)^2+b$,$D:y=-x^2$ より $y$ を消去すると
\begin{align*}
&(x-a)^2+x^2+b=0 \\[4pt]
&2x^2-2ax+a^2+b=0~\cdots\cdots①
\end{align*}
$C$ と $D$ が異なる2点で交わるから,①は異なる2つの実数解をもつ。このとき①の判別式を $D$ とすると,$D>0$ が成り立つから&(x-a)^2+x^2+b=0 \\[4pt]
&2x^2-2ax+a^2+b=0~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{D}{4}=a^2-2(a^2+b)>0 \\[4pt]
&-a^2-2b>0 \\[4pt]
&b<=-\dfrac{1}{2}a^2~\cdots\cdots② \end{align*}
$C$ と $D$ が異なる2点で交わるだけなら,点 $(a,~b)$ は放物線 $y=-\dfrac{1}{2}x^2$ の下側にあることになる。しかし,$C$ と $D$ の交点について条件があるから,点 $(a,~b)$ の存在範囲は放物線 $y=-\dfrac{1}{2}x^2$ の下側すべてではないだろう。それは「軌跡を求めよ。」とあることからも予想できる。与えられた条件から,点 $(a,~b)$ の存在範囲を求めよう。&\dfrac{D}{4}=a^2-2(a^2+b)>0 \\[4pt]
&-a^2-2b>0 \\[4pt]
&b<=-\dfrac{1}{2}a^2~\cdots\cdots② \end{align*}
$C$ と $D$ の2交点の $x$ 座標の差が1であるから,①の2解を $\alpha,~\alpha+1$ とおくと,解と係数の関係より
\begin{align*} &\alpha+(\alpha+1)=a~\cdots\cdots③ \\[4pt] &\alpha(\alpha+1)=\dfrac{a^2+b}{2}~\cdots\cdots④ \end{align*}
③より,$\alpha=\dfrac{a-1}{2}$ ④より \begin{align*} b&=2\alpha(\alpha+1)-a^2 \\[4pt] &=2\Cdota\dfrac{a-1}{2}\Cdota\dfrac{a+1}{2}-a^2 \\[4pt] &=-\dfrac{1}{2}a^2-\dfrac{1}{2} \end{align*}
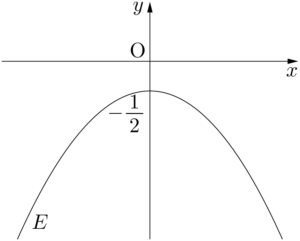
これは②をみたす。 したがって,求める点 $(a,~b)$ の軌跡は,放物線 $E:y=-\dfrac{1}{2}x^2-\dfrac{1}{2}$ であり,下図のようになる。
(2) 実数 $a,~b$ が(1)の条件を満たしながら動くとき,$C$ と $D$ の2交点を結ぶ直線が通過する領域を求め,図示せよ。
【(2)の考え方と解答】
$C:y=(x-a)^2+b$,$D:y=-x^2$ より $x^2$ を消去すると,

$C:y=(x-a)^2+b$,$D:y=-x^2$ より $x^2$ を消去すると,
\begin{align*} &2y=(x-a)^2-x^2+b \\[4pt] &2y=-a(2x-a)+b \\[4pt] &2ax+2y-a^2-b=0~\cdots\cdots⑤ \end{align*}
となり,⑤が $C$ と $D$ の2交点を結ぶ直線の方程式である。$a,~b$ が(1)の条件をみたしながら動くとき,$b=-\dfrac{1}{2}a^2-\dfrac{1}{2}$ が成り立つから,⑤に代入すると \begin{align*} &2ax+2y-a^2+\dfrac{1}{2}a^2+\dfrac{1}{2}=0 \\[4pt] &4ax+4y-a^2+1=0~\cdots\cdots⑥ \end{align*}
直線⑥が点 $(X,~Y)$ を通るとすると \begin{align*} 4aX+4Y-a^2+1=0 \end{align*}
が成り立つ。これを $a$ の方程式とみると \begin{align*} a^2-4Xa-4Y-1=0~\cdots\cdots⑦ \end{align*}
となり,$a$ は実数であるから,⑦は実数解をもつ。判別式を $D_2$ とすると $D_2\geqq0$ となるから \begin{align*} &\dfrac{D_2}{4}=4X^2+4Y+1\geqq0 \\[4pt] &Y\geqq-X^2-\dfrac{1}{4} \end{align*}
よって,求める領域は放物線 $F:y=-x^2-\dfrac{1}{4}$ の上側であり,下図の斜線部分(境界を含む)となる。

ヒロ
下のアニメーションを見ることで,直線⑥が放物線 $y=-x^2-\dfrac{1}{4}$ に接しながら動いていることが確認できる。


















