楕円は,2つの定点までの距離の和が一定である点の軌跡として定義されます。また,その2つの定点を焦点といいます。楕円の焦点の座標は,覚えにくいものの1つかもしれませんが,定義をしっかり考えることで,楕円の焦点の座標も簡単に覚えることができるでしょう。
また,楕円の極方程式の導出は,一度は見ておいた方が良いかもしれません。
Contents
楕円の方程式の導出

ヒロ
楕円の方程式を求めよう。
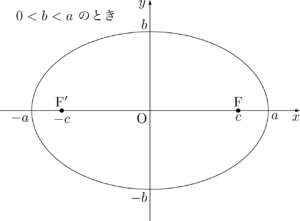
2つの焦点を $\mathrm{F}(c,~0)$, $\mathrm{F}'(-c,~0)$ $(c>0)$ とし,楕円上の点を $\mathrm{P}(x,~y)$ とする。$\mathrm{PF}+\mathrm{PF’}=2a~(a>c>0)$ とすると,
また,焦点の座標を $a,~b$ で表すと
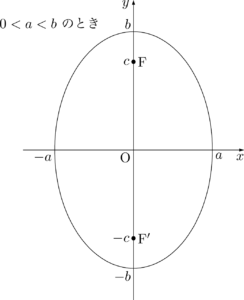
$a,~b$ の大小関係を入れ替えると,焦点は $y$ 軸上の点となり,縦長の楕円となる。
\begin{align*}
&\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \\[4pt]
&\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}
\end{align*}
両辺を2乗すると&\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \\[4pt]
&\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}
\end{align*}
\begin{align*}
&(x-c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \\[4pt]
&4a\sqrt{(x+c)^2+y^2}=4cx+4a^2 \\[4pt]
&a\sqrt{(x+c)^2+y^2}=cx+a^2
\end{align*}
さらに両辺を2乗すると&(x-c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \\[4pt]
&4a\sqrt{(x+c)^2+y^2}=4cx+4a^2 \\[4pt]
&a\sqrt{(x+c)^2+y^2}=cx+a^2
\end{align*}
\begin{align*}
&a^2\{(x+c)^2+y^2\}=c^2x^2+2ca^2x+a^4 \\[4pt]
&(a^2-c^2)x^2+a^2y^2=a^4-a^2c^2 \\[4pt]
&\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1
\end{align*}
ここで,$a^2-c^2=b^2$ とおくと,楕円の方程式は&a^2\{(x+c)^2+y^2\}=c^2x^2+2ca^2x+a^4 \\[4pt]
&(a^2-c^2)x^2+a^2y^2=a^4-a^2c^2 \\[4pt]
&\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1
\end{align*}
\begin{align*}
&\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1~(0<b<a)
\end{align*}
となり,グラフは図のようになる。&\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1~(0<b<a)
\end{align*}

また,焦点の座標を $a,~b$ で表すと
\begin{align*}
\mathrm{F}(\sqrt{a^2-b^2},~0),~~\mathrm{F}'(-\sqrt{a^2-b^2},~0)
\end{align*}
となる。\mathrm{F}(\sqrt{a^2-b^2},~0),~~\mathrm{F}'(-\sqrt{a^2-b^2},~0)
\end{align*}
$a,~b$ の大小関係を入れ替えると,焦点は $y$ 軸上の点となり,縦長の楕円となる。



















