Contents
2019年 星薬科大
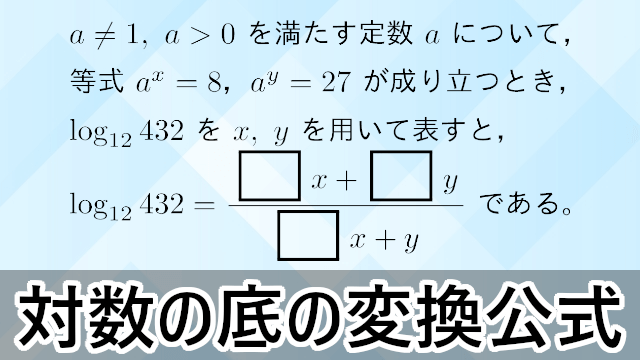
2019年 星薬科大$a\neq1,~a>0$ を満たす定数 $a$ について,等式 $a^x=8$,$a^y=27$ が成り立つとき,$\log_{12}432$ を $x,~y$ を用いて表すと,$\log_{12}432=\dfrac{\myhako\,x+\myhako\,y}{\myhako\,x+y}$ である。
【考え方と解答】
$a^x=8$ より
$a^x=8$ より
\begin{align*}
x=\log_a8=3\log_a2
\end{align*}
$a^y=27$ よりx=\log_a8=3\log_a2
\end{align*}
\begin{align*}
y=\log_a27=3\log_a3
\end{align*}
12と432を2と3で表すとy=\log_a27=3\log_a3
\end{align*}
\begin{align*}
&12=2^2\Cdota3 \\[4pt]
&432=2^4\Cdota3^3
\end{align*}
となるから&12=2^2\Cdota3 \\[4pt]
&432=2^4\Cdota3^3
\end{align*}
\begin{align*}
\log_{12}432&=\dfrac{\log_a432}{\log_a12} \\[4pt]
&=\dfrac{\log_a(2^4\Cdot3^3)}{\log_a(2^2\Cdot3)} \\[4pt]
&=\dfrac{4\log_a2+3\log_a3}{2\log_a2+\log_a3} \\[4pt]
&=\dfrac{\frac{4}{3}x+y}{\frac{2}{3}x+\frac{1}{3}y} \\[4pt]
&=\dfrac{4x+3y}{2x+y}
\end{align*}
\log_{12}432&=\dfrac{\log_a432}{\log_a12} \\[4pt]
&=\dfrac{\log_a(2^4\Cdot3^3)}{\log_a(2^2\Cdot3)} \\[4pt]
&=\dfrac{4\log_a2+3\log_a3}{2\log_a2+\log_a3} \\[4pt]
&=\dfrac{\frac{4}{3}x+y}{\frac{2}{3}x+\frac{1}{3}y} \\[4pt]
&=\dfrac{4x+3y}{2x+y}
\end{align*}
2018年 立命館大
2019年 立命館大$a,~b$ を1以外の正の数とする。式
\begin{align*}
(\log_ab+\log_{a^n}b^n)(\log_ba^n+\log_{b^n}a)
\end{align*}
を $n$ のみを用いて表すと $\myhako$ となる。(\log_ab+\log_{a^n}b^n)(\log_ba^n+\log_{b^n}a)
\end{align*}
【考え方と解答】
その都度,都合がよくなるように底を変えて計算しよう。
その都度,都合がよくなるように底を変えて計算しよう。
\begin{align*}
&(\log_ab+\log_{a^n}b^n)(\log_ba^n+\log_{b^n}a) \\[4pt]
&=(\log_ab+\log_ab)\left(n\log_ba+\dfrac{1}{n}\log_ba\right) \\[4pt]
&=2\log_ab\Cdota\left(n+\dfrac{1}{n}\right)\log_ba \\[4pt]
&=2\left(n+\dfrac{1}{n}\right)
\end{align*}
&(\log_ab+\log_{a^n}b^n)(\log_ba^n+\log_{b^n}a) \\[4pt]
&=(\log_ab+\log_ab)\left(n\log_ba+\dfrac{1}{n}\log_ba\right) \\[4pt]
&=2\log_ab\Cdota\left(n+\dfrac{1}{n}\right)\log_ba \\[4pt]
&=2\left(n+\dfrac{1}{n}\right)
\end{align*}