ここでは双心四角形の面積について説明します。
三角形はその形状によらず,常に,外接円・内接円を描くことができます。
しかし,四角形の場合は,外接円や内接円が存在するためには,特別な条件が必要です。
円に内接する四角形の面積を求める公式として,ブラーマグプタの公式が知られています。
この記事で扱う「双心四角形」とは外接円と内接円の両方をもつ四角形のことです。
四角形が円に内接するときの条件に加えて,円に外接するときの条件も満たす必要があります。
どのような条件が必要なのか,また,そのときの四角形の面積はどのように表されるかを学びましょう。
四角形が円に外接するための条件

ヒロ
四角形が円に外接するための条件を考えよう。
【四角形が円に外接するための条件】
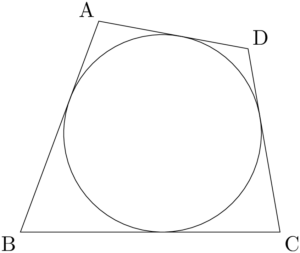
次の図のように,四角形ABCDが円に外接する条件を考える。
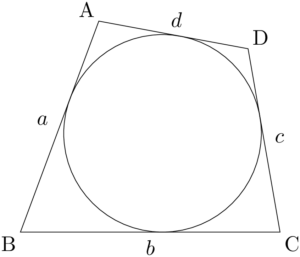
四角形ABCDとその内接円との接点をP, Q, R, Sとする。
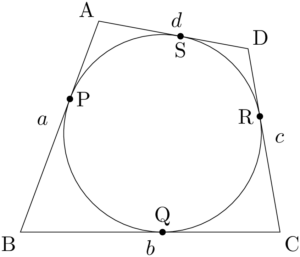
円の外部の点から円に接線を引いたとき,接線の長さは等しいから,次の図のように同じ印を付けた線分の長さが等しくなる。
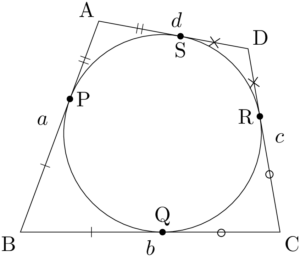
このとき,付けた印に着目すると対辺の長さの和が等しいことが分かる。つまり,四角形ABCDが円に外接するための条件は
次の図のように,四角形ABCDが円に外接する条件を考える。

四角形ABCDとその内接円との接点をP, Q, R, Sとする。

円の外部の点から円に接線を引いたとき,接線の長さは等しいから,次の図のように同じ印を付けた線分の長さが等しくなる。

このとき,付けた印に着目すると対辺の長さの和が等しいことが分かる。つまり,四角形ABCDが円に外接するための条件は
\begin{align*}
a+c=b+d
\end{align*}
が成り立つことである。a+c=b+d
\end{align*}
四角形ABCDが円に外接するための条件四角形ABCDが円に外接するための条件は
\begin{align*}
\text{AB}+\text{CD}=\text{AD}+\text{BC}
\end{align*}
が成り立つことである。\text{AB}+\text{CD}=\text{AD}+\text{BC}
\end{align*}

円に外接する四角形の面積

ヒロ
円に外接する四角形の面積を求めてみよう。
【円に外接する四角形の面積】
次の図のように,四角形ABCDが円に外接するときの面積 $S$ を求める。

ブレートシュナイダーの公式より,$s=\dfrac{a+b+c+d}{2}$ とおくと
次の図のように,四角形ABCDが円に外接するときの面積 $S$ を求める。

ブレートシュナイダーの公式より,$s=\dfrac{a+b+c+d}{2}$ とおくと
\begin{align*}
S&=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}}
\end{align*}
と表される。ここで,$a+c=b+d$ が成り立つから $s=\dfrac{a+b+c+d}{2}$ よりS&=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}}
\end{align*}
\begin{align*}
a+c=b+d=s
\end{align*}
となる。これよりa+c=b+d=s
\end{align*}
\begin{align*}
&s-a=c \\[4pt]
&s-b=d \\[4pt]
&s-c=a \\[4pt]
&s-d=b
\end{align*}
となる。したがって&s-a=c \\[4pt]
&s-b=d \\[4pt]
&s-c=a \\[4pt]
&s-d=b
\end{align*}
\begin{align*}
S&=\sqrt{abcd-abcd\cos^2\dfrac{A+C}{2}} \\[4pt]
&=\sqrt{abcd\left(1-\cos^2\dfrac{A+C}{2}\right)} \\[4pt]
&=\sqrt{abcd\sin^2\dfrac{A+C}{2}} \\[4pt]
&=\sqrt{abcd}\sin\dfrac{A+C}{2}
\end{align*}
S&=\sqrt{abcd-abcd\cos^2\dfrac{A+C}{2}} \\[4pt]
&=\sqrt{abcd\left(1-\cos^2\dfrac{A+C}{2}\right)} \\[4pt]
&=\sqrt{abcd\sin^2\dfrac{A+C}{2}} \\[4pt]
&=\sqrt{abcd}\sin\dfrac{A+C}{2}
\end{align*}
円に外接する四角形の面積円に外接する四角形ABCDの面積は

\begin{align*}
S=\sqrt{abcd}\sin\dfrac{A+C}{2}
\end{align*}
と表される。S=\sqrt{abcd}\sin\dfrac{A+C}{2}
\end{align*}

双心四角形であるための条件と面積

ヒロ
四角形が外接円と内接円の両方をもつときの条件とその面積を求めよう。
【双心四角形の面積】
四角形ABCDが円に内接するとき,対角の和が180°である。また,四角形ABCDが円に外接するとき,対辺の長さの和が等しい。したがって,これら2つの条件をみたす四角形が双心四角形である。

四角形ABCDは円に外接するから,その面積 $S$ は
四角形ABCDが円に内接するとき,対角の和が180°である。また,四角形ABCDが円に外接するとき,対辺の長さの和が等しい。したがって,これら2つの条件をみたす四角形が双心四角形である。

四角形ABCDは円に外接するから,その面積 $S$ は
\begin{align*}
S=\sqrt{abcd}\sin\dfrac{A+C}{2}
\end{align*}
と表される。さらに,四角形ABCDは円に内接するから対角の和が180°である,すなわち $A+C=180\Deg$ である。したがってS=\sqrt{abcd}\sin\dfrac{A+C}{2}
\end{align*}
\begin{align*}
S&=\sqrt{abcd}\sin\dfrac{180\Deg}{2} \\[4pt]
&=\sqrt{abcd}\sin90\Deg \\[4pt]
&=\sqrt{abcd}
\end{align*}
S&=\sqrt{abcd}\sin\dfrac{180\Deg}{2} \\[4pt]
&=\sqrt{abcd}\sin90\Deg \\[4pt]
&=\sqrt{abcd}
\end{align*}
双心四角形の面積双心四角形ABCDの面積は

\begin{align*}
S=\sqrt{abcd}
\end{align*}
と表される。S=\sqrt{abcd}
\end{align*}