ここではブレートシュナイダーの公式について説明します。
円に内接する四角形の面積を求める公式として,ブラーマグプタの公式が知られていますが,それを一般化したものがブレートシュナイダーの公式です。
つまり,ブレートシュナイダーの公式を利用することで,任意の四角形の面積を求めることができるようになります。
記事の内容を理解するためには,次の記事で説明している「加法定理」や「2倍角の公式」を知っている必要があります。
ブレートシュナイダーの公式

ヒロ
ブレートシュナイダーの公式とは次のようなものである。
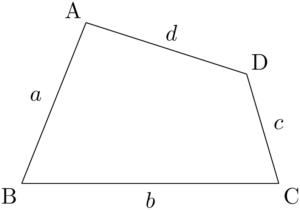
ブレートシュナイダーの公式4点A, B, C, Dがあり,$\text{AB}=a$, $\text{BC}=b$, $\text{CD}=c$, $\text{DA}=d$ とする。$s=\dfrac{a+b+c+d}{2}$とすると,四角形ABCDの面積 $S$ は,
\begin{align*}
S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}}
\end{align*}
と表される。S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}}
\end{align*}

四角形の面積と対角線のなす角

ヒロ
ブレートシュナイダーの公式を導くために,四角形の面積を対角線の長さを用いて表す。
【四角形の面積】
次の図のように,四角形ABCDの対角線のなす角を $\theta$ とし,対角線の長さを $x,~y$ とする。
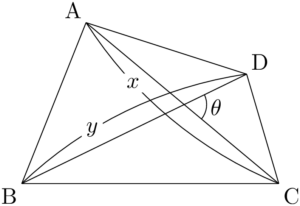
このとき,四角形ABCDの面積 $S$ を $x,~y,~\sin\theta$ で表そう。
ACとBDの交点をEとし,Eで分けられたそれぞれの線分の長さを $p,~q,~r,~s$ とする。
$\sankaku{ADE}$, $\sankaku{CDE}$, $\sankaku{ABE}$, $\sankaku{BCE}$ の面積を求めると次のようになる。
次の図のように,四角形ABCDの対角線のなす角を $\theta$ とし,対角線の長さを $x,~y$ とする。

このとき,四角形ABCDの面積 $S$ を $x,~y,~\sin\theta$ で表そう。
ACとBDの交点をEとし,Eで分けられたそれぞれの線分の長さを $p,~q,~r,~s$ とする。
$\sankaku{ADE}$, $\sankaku{CDE}$, $\sankaku{ABE}$, $\sankaku{BCE}$ の面積を求めると次のようになる。
\begin{align*}
\sankaku{ADE}&=\dfrac{1}{2}pr\sin(180\Deg-\theta) \\[4pt]
&=\dfrac{1}{2}pr\sin\theta \\[4pt]
\sankaku{CDE}&=\dfrac{1}{2}qr\sin\theta \\[4pt]
\sankaku{ABE}&=\dfrac{1}{2}ps\sin\theta \\[4pt]
\sankaku{BCE}&=\dfrac{1}{2}qs\sin(180\Deg-\theta) \\[4pt]
&=\dfrac{1}{2}qs\sin\theta
\end{align*}
したがって,\sankaku{ADE}&=\dfrac{1}{2}pr\sin(180\Deg-\theta) \\[4pt]
&=\dfrac{1}{2}pr\sin\theta \\[4pt]
\sankaku{CDE}&=\dfrac{1}{2}qr\sin\theta \\[4pt]
\sankaku{ABE}&=\dfrac{1}{2}ps\sin\theta \\[4pt]
\sankaku{BCE}&=\dfrac{1}{2}qs\sin(180\Deg-\theta) \\[4pt]
&=\dfrac{1}{2}qs\sin\theta
\end{align*}
\begin{align*}
S&=\sankaku{ADE}+\sankaku{CDE}+\sankaku{ABE}+\sankaku{BCE} \\[4pt]
&=\dfrac{1}{2}pr\sin\theta+\dfrac{1}{2}qr\sin\theta+\dfrac{1}{2}ps\sin\theta+\dfrac{1}{2}qs\sin\theta \\[4pt]
&=\dfrac{1}{2}(p+q)r\sin\theta+\dfrac{1}{2}(p+q)s\sin\theta \\[4pt]
&=\dfrac{1}{2}xr\sin\theta+\dfrac{1}{2}xs\sin\theta \\[4pt]
&=\dfrac{1}{2}x(r+s)\sin\theta \\[4pt]
&=\dfrac{1}{2}xy\sin\theta
\end{align*}
S&=\sankaku{ADE}+\sankaku{CDE}+\sankaku{ABE}+\sankaku{BCE} \\[4pt]
&=\dfrac{1}{2}pr\sin\theta+\dfrac{1}{2}qr\sin\theta+\dfrac{1}{2}ps\sin\theta+\dfrac{1}{2}qs\sin\theta \\[4pt]
&=\dfrac{1}{2}(p+q)r\sin\theta+\dfrac{1}{2}(p+q)s\sin\theta \\[4pt]
&=\dfrac{1}{2}xr\sin\theta+\dfrac{1}{2}xs\sin\theta \\[4pt]
&=\dfrac{1}{2}x(r+s)\sin\theta \\[4pt]
&=\dfrac{1}{2}xy\sin\theta
\end{align*}

ヒロ
四角形の面積の公式として使えるようにしておこう。
四角形の面積公式次の図の四角形ABCDの面積 $S$ は

\begin{align*}
S=\dfrac{1}{2}xy\sin\theta
\end{align*}
と表される。S=\dfrac{1}{2}xy\sin\theta
\end{align*}

ブレートシュナイダーの公式の導出

ヒロ
それではブレートシュナイダ―の公式を導出しよう。
【ブレートシュナイダーの公式の導出】
次の図のような四角形ABCDを考える。

対角線BDを引いて2つの三角形に分割する。
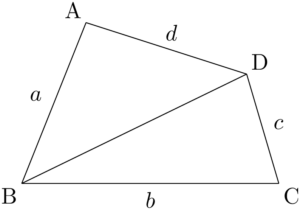
このとき四角形ABCDの面積 $S$ は
次の図のような四角形ABCDを考える。

対角線BDを引いて2つの三角形に分割する。

このとき四角形ABCDの面積 $S$ は
\begin{align*}
S&=\sankaku{ABD}+\sankaku{BCD} \\[4pt]
&=\dfrac{1}{2}ad\sin A+\dfrac{1}{2}bc\sin C
\end{align*}
と表せるからS&=\sankaku{ABD}+\sankaku{BCD} \\[4pt]
&=\dfrac{1}{2}ad\sin A+\dfrac{1}{2}bc\sin C
\end{align*}
\begin{align*}
4S^2&=(ad\sin A+bc\sin C)^2 \\[4pt]
&=a^2d^2\sin^2A+b^2c^2\sin^2C+2abcd\sin A\sin C~\cdots\cdots①
\end{align*}
ここで,$\sankaku{ABD}$ と $\sankaku{BCD}$ において,余弦定理より4S^2&=(ad\sin A+bc\sin C)^2 \\[4pt]
&=a^2d^2\sin^2A+b^2c^2\sin^2C+2abcd\sin A\sin C~\cdots\cdots①
\end{align*}
\begin{align*}
y^2=a^2+d^2-2ad\cos A=b^2+c^2-2bc\cos C
\end{align*}
であるからy^2=a^2+d^2-2ad\cos A=b^2+c^2-2bc\cos C
\end{align*}
\begin{align*}
&a^2+d^2-b^2-c^2=2ad\cos A-2bc\cos C \\[4pt]
&\dfrac{1}{2}(a^2+d^2-b^2-c^2)=ad\cos A-bc\cos C
\end{align*}
両辺を2乗すると&a^2+d^2-b^2-c^2=2ad\cos A-2bc\cos C \\[4pt]
&\dfrac{1}{2}(a^2+d^2-b^2-c^2)=ad\cos A-bc\cos C
\end{align*}
\begin{align*}
&\dfrac{1}{4}(a^2+d^2-b^2-c^2)^2=(ad\cos A-bc\cos C)^2 \\[4pt]
&=a^2d^2\cos^2A+b^2c^2\cos^2C-2abcd\cos A\cos C~\cdots\cdots②
\end{align*}
$①+②$ より&\dfrac{1}{4}(a^2+d^2-b^2-c^2)^2=(ad\cos A-bc\cos C)^2 \\[4pt]
&=a^2d^2\cos^2A+b^2c^2\cos^2C-2abcd\cos A\cos C~\cdots\cdots②
\end{align*}
\begin{align*}
&4S^2+\dfrac{1}{4}(a^2+d^2-b^2-c^2)^2=a^2d^2+b^2c^2-2abcd(\cos A\cos C-\sin A\sin C)
\end{align*}
加法定理より $\cos A\cos C-\sin A\sin C=\cos(A+C)$ であるから&4S^2+\dfrac{1}{4}(a^2+d^2-b^2-c^2)^2=a^2d^2+b^2c^2-2abcd(\cos A\cos C-\sin A\sin C)
\end{align*}
\begin{align*}
&16S^2=4a^2d^2+4b^2c^2-(a^2+d^2-b^2-c^2)^2-8abcd\cos(A+C)
\end{align*}
2倍角の公式より $\cos(A+C)=2\cos^2\dfrac{A+C}{2}-1$ であるから&16S^2=4a^2d^2+4b^2c^2-(a^2+d^2-b^2-c^2)^2-8abcd\cos(A+C)
\end{align*}
\begin{align*}
&16S^2=(2ad+2bc)^2-8abcd-(a^2+d^2-b^2-c^2)^2-8abcd\left(2\cos^2\dfrac{A+C}{2}-1\right) \\[4pt]
&16S^2=(2ad+2bc)^2-(a^2+d^2-b^2-c^2)^2-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&16S^2=(2ad+2bc+a^2+d^2-b^2-c^2)(2ad+2bc-a^2-d^2+b^2+c^2)-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&16S^2=\{(a+d)^2-(b-c)^2\}\{(b+c)^2-(a-d)^2\}-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&16S^2=(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)-16abcd\cos^2\dfrac{A+C}{2}
\end{align*}
ここで $\dfrac{a+b+c+d}{2}=s$ とおくと&16S^2=(2ad+2bc)^2-8abcd-(a^2+d^2-b^2-c^2)^2-8abcd\left(2\cos^2\dfrac{A+C}{2}-1\right) \\[4pt]
&16S^2=(2ad+2bc)^2-(a^2+d^2-b^2-c^2)^2-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&16S^2=(2ad+2bc+a^2+d^2-b^2-c^2)(2ad+2bc-a^2-d^2+b^2+c^2)-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&16S^2=\{(a+d)^2-(b-c)^2\}\{(b+c)^2-(a-d)^2\}-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&16S^2=(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)-16abcd\cos^2\dfrac{A+C}{2}
\end{align*}
\begin{align*}
&16S^2=(2s-2c)(2s-2b)(2s-2d)(2s-2a)-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&S^2=(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}
\end{align*}
$S>0$ であるから&16S^2=(2s-2c)(2s-2b)(2s-2d)(2s-2a)-16abcd\cos^2\dfrac{A+C}{2} \\[4pt]
&S^2=(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}
\end{align*}
\begin{align*}
S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}}
\end{align*}
S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\dfrac{A+C}{2}}
\end{align*}



















